Определение скорости и ускорения точки при координатном способе задания ее движения

Если движение точки задано в координатной форме, то каждое параметрическое уравнений , взятое отдельно, описывает движение не самой точки, а ее проекции вдоль соответствующих осей. Пусть движение точки А в плоской системе координат задано уравнениями

х =f₁ (t) и у =f₂ (t).

Первое из уравнений определяет закон изменения абсциссы х движущейся точки (рис. 1.118), т. е. описывает движе­ние по оси абсцисс точки А_х — проекции точки А на ось х. Второе уравнение определяет закон изменения ординаты у точки А, т. е. описывает движение по оси ординат ее проекции А_у на эту ось. Допустим, что в данный момент времени t точка А имеет скорость v , тогда А_х и А у — проекции точки на оси х и у—движутся по осям со скоростями v_х и v_у, модули которых равны проекциям скорости v на соответст­вующие оси (рис. 10.5). Следовательно, дифферен­цируя каждое из заданных уравнений, найдем модули скоростей v_x и v_у или, иначе говоря, проекции скорости v на оси координат.

Итак,

v_x = dx/dt =f'(t) и v_y = dy/dt = f'(t). (1.100)

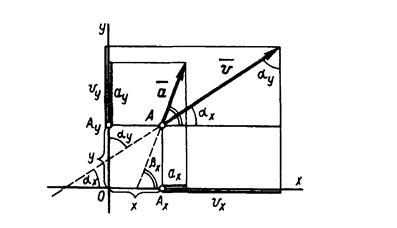
Рис 10.5

Если из начала и конца вектора v провести прямые, параллельные осям координат, то получим прямоугольный треугольник с гипотенузой v и кате­тами v_х и v_y . Отсюда модуль искомой скорости

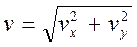(1.101)

Направление скорости v, т. е. углы α_х или α_у , находим по одной из следующих формул:

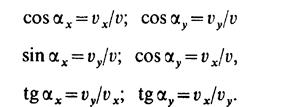
Аналогично определяется и вектор ускорения а. Сначала находим его проекции на оси х и у:

а_х = dv_x/dt =f"(t) и а_у = dv_у /dt =f"(t), (1.105)

а затем модуль

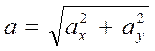(1.106)

и направление, т. е. углы β_х и β_y (угол β_у на рис. 1.118 не обозначен):

От координатного способа задания движения точки нетрудно перейти к естественному способу. Ранее мы рассмотрели , что, исключив время из уравнений движения х =f₁ (t),

у =f₂ (t), получаем уравнение тра­ектории Ф (х, у) = 0. Уравнение движения S =f(t) по этой траектории получаем следующим образом. Так как v = dS / dt то dS = v dt; подставив сюда значение 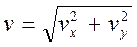полученное из уравнений движения в

осях координат, и проинтегрировав:

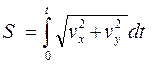(1.108)

получим уравнения движения вида S =f(t).

Например, если движение точки задано уравне­ниями х = 3t² и у = 4t², то точка движется по прямолинейной траектории, уравнение которой 4x – 3y = 0.

Из заданных уравнений движения следует, что проекции скорости на оси координат

V_X = 6t V_у = 8t ,

а модуль скорости в любой момент времени

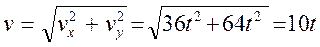
Из уравнения (1.108)

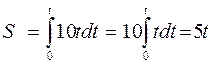
Таким образом, точка движется прямолинейно по траектории 4х— 3y = 0 согласно уравнению S = 5t².

ЛЕКЦИЯ 11