Момент імпульсу. закон збереження моменту імпульсу

З рівняння (5) маємо:

.

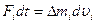Домноживши обидві частини цього рівняння на 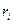, одержимо:

.

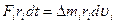При постійних 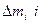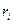можна записати так:

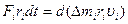. (7)

Добуток імпульсу елемента маси 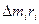на відстань від вісі обертання до елемента маси називається моментом імпульсу.

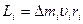(8)

Просумуємо рівняння виду (7) для всіх елементів тіла. Знайдемо:

;

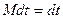Дій 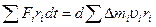(9)

Де 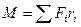сумарний обертовий момент, що діє на тіло.

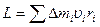- момент імпульсу всього тіла (момент кількості руху). Можна записати так:

,

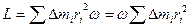або L = Iw, або 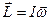(10)

Момент імпульсу - це вектор, направлений по вісі обертання у відповідності з правилом правого гвинта. Таким чином, вектор моменту імпульсу співпадає з напрямом вектора кутової швидкості.

Таким чином, момент імпульсу тіла дорівнює добутку моменту інерції тіла на кутову швидкість. Рівняння (9) можна записати так:

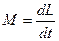. (11)

або у векторній формі

.

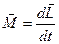Це рівняння називається рівнянням моментів.

Якщо на тіло діють сили або сумарний обертовий момент дорівнює нулю, тоді маємо:

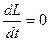або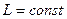

В цьому і полягає закон збереження моменту імпульсу. Його можна записати так:

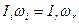(12)

Момент імпульсу замкнутої системи зберігається, тобто, не змінюється з плином часу.

Цей закон використовується спортсменами при виконанні стрибка через голову.

Роль імпульсу тіла при обертальному рухові відіграє момент імпульсу. Момент імпульсу пов’язаний з певною властивістю симетрії простору - його ізотропністю, тобто з інваріантністю фізичних законів відносно вибору напрямків вісей координат системи відліку (відносно повороту замкнутої системи в просторі на будь-який кут).

Поступальний рух	Обертальний рух
Маса m	Момент інерції J
Шлях S	Кут оберту j
Швидкість	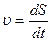Кутова швидкість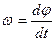
Імпульс	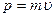Момент імпульсу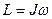
Прискорення	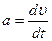Кутове прискорення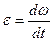
Рівнодіюча зовнішніх сил	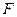Сума моментів зовнішніх сил
Основне рівняння динаміки	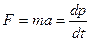Основне рівняння динаміки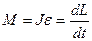
Робота FdS	Робота обертання Mdj
Кінетична енергія	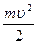Кінетична енергія обертання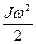

Закон збереження моменту імпульсу - фундаментальний закон природи.