Характеристика систем счисления
| Вид | Алфавит | Основание | На калькуляторе |
| двоичная | 0,1 | BIN I | |
| восьмеричная | 0,1,2,3,4,5,6,7 | OCT G | |
| десятичная | 0,1,2,3,4,5,6,7,8,9 | DEG + | |
| шестнадцатеричная | 0,1,2,3,4,5,6,7,8,9, А,B.C,D,E,F | HEX G |
Запись чисел в каждой из систем счисления с основанием n можно представить виде полинома
Х = аn кn + а n-1 кn-1 +……+а1 к1+ а 0 к0 ;
где х – число;
к – основание системы счисления;
аn, а n-1…….. а1 а 0 – последовательность цифр;
Расширенная запись числа – это сумма произведения коэффициентов на основание системы счисления в степени позиции цифры в числе.
Например : 41810 ,где 10 – основание системы счисления
Алгоритм перевода
Алгоритм - точный порядок, правил, команд, указаний, действий определяющий процесс ведущий от исходных данных к исходному результату.
Распишем разряды. Разряды подписываются от младшего к старшему справа на лево; младший разряд 0, любое число в степени 0=1, а в степени 1 = этому числу.
418 = 4 *102 + 1* 101+ 8*100 = 400 +10+8
Электронные блоки компьютера могут обрабатывать информацию только в цифровом виде. ПК используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
- для реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток – нет тока, намагничен и т.п.), а не с десятью, как десятичной;
- представление информации посредством только двух состояний надежно и помехоустойчиво;
- возможно применение булевой алгебры для выполнения логических преобразований информации;
- двоичная арифметика намного проще десятичной.
Недостаток – быстрый рост числа разрядов, необходимых для записи чисел, особенно для человека из - за громоздкости и непривычной записи.
В ПК используются восьмеричная и шестнадцатеричная системы счисления. Числа в этих системах, читаются почти также легко как в десятичной, требуют соответственно в три (восьмеричная) и четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и16 соответственно третья и четвертая степень числа 2).
Перевод чисел из десятичной в двоичную систему счисления и наоборот выполняет ПК.
Перевод чисел из десятичной системы счисления в систему счисления с основанием к
Алгоритм перевода
1.Число делится на к остаток записывается;
2.Частное вновь делится к остаток записывается;
3. Процедура повторяется пока частное не станет меньше к
или равно нулю;
4 Остатки выписываются справа на лево, в порядке их получения.
Например: число 4610 перевести в систему счисления с основанием к =2
| |
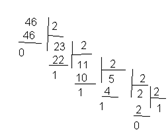
Записываем число справа налево 1011102 = 4610 проверим по полиному распишем разряды
543210 х = 1*25 + 0*24+ 1*23+1*22 +1*21 + 0*20 =32+8+4+2=4610
Например: число 6810 перевести в систему счисления с основанием к =8
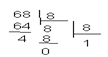
Записываем число справа налево 1048
Например: число 4610 перевести в систему счисления с основанием к =16
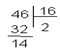
Записываем число справа налево 214
14 по алфавиту шестнадцатеричной системы счисления буква Е значит получаем число 2Е16. Проверим по полиному:
2Е х =2*161+ 14*160= 32+14 = 4610
Дата добавления: 2015-08-08; просмотров: 1718;
