Свойства бегущих волн

Запишем уравнение (3.47) в виде:

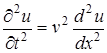. (3.50)

где v— скорость перемещения величины и вдоль оси х. Это уравнение было получено для упругих волн в сплошной струне, но оно не содержит какой-либо специфики упругих волн, а выражает лишь волновой характер изменения физической величины u(x,t) во времени и пространстве. Поэтому, если под величиной v понимать скорость этого изменения, то данное уравнение можно рассматривать как общий вид волнового уравнения для произвольной физической величины u(х, t).

Решением волнового уравнения согласно (3.48) является периодическая по времени и координате функция

u(x,t) = u×cos[ω(t–x/v)+a], (3.51)

которая представляет собой бегущую волну, осуществляющую перенос фазы колебания величины и с постоянной скоростью u вдоль направления распространения волны. Расстояние, на которое перемещается фаза за один период колебания Т, l = v×T называется длиной волны. Удобно для описания волны пользоваться угловыми переменными – угловой частотой ω = 2p/T и волновым числом k = 2p/l. Скорость перемещения фазы может быть выражена через эти величины

v = v_ф =l/T = ω/k (3.52)

и называется фазовой скоростью волны. Заменив в уравнении (3.51) скорость на фазовую, запишем уравнение бегущей волны в виде:

u(x,t) = u×cos(ωt – kx + a). (3.53)

Это уравнение представляет собой наиболее часто употребляемый вид бегущей волны, распространяющейся вдоль оси x.

При распространении волны в сплошной среде колебания испытывает одновременно большое число частиц. Геометрическое место точек, колеблющихся в одинаковой фазе, образует волновую поверхность. Например, в случае волны (3.53), распространяющейся вдоль оси x, волновыми поверхностями являются любые плоскости x = const. Такая волна называется плоской. Поверхность, отделяющая колеблющиеся частицы от остальной области пространства, которой колебания еще не достигли, — фронт волны.

Выше была рассмотрена волна, которая распространялась вдоль оси x . Это случай одномерного распространения, так как положение колеблющейся частицы определяется заданием только одной величины — ее координаты х. Волна может распространяться на плоскости — это случай двухмерного распространения. Наконец, волна может распространяться в трехмерном пространстве. Довольно частой является ситуация, когда источник колебаний локализован в малой области пространства или сосредоточен, а волна распространяется во все стороны от него. Если свойства среды, в которой распространяется волна, одинаковы по всем направлениям, то скорость волны во всех направлениях будет одна и та же, и все волновые поверхности, включая и фронт волны, будут представлять собой сферы с центром в точке нахождения источника колебаний. Такую волну называют сферической. На больших расстояниях от источника, когда радиус сферы, определяющей фронт волны, становится очень большим, участки волнового фронта с размерами, много меньшими расстояния до источника, можно рассматривать как плоские, т. е. считать сферическую волну плоской. Это приближение используется при решении многих задач.

Нетрудно написать уравнение сферической волны. Положение колеблющейся частицы определяется в этом случае только ее расстоянием от источника колебаний r, т.е. фаза колебаний должна иметь вид ωt – kr + a. Амплитуда колебаний в сферической волне, однако, не будет оставаться постоянной — она убывает с расстоянием, как 1/r. Последнее утверждение вытекает из требования, чтобы поток энергии, переносимый волной через поверхность сферы любого, сколь угодно большого, радиуса оставался постоянным. Таким образом, сферическая волна должна иметь следующий вид:

u(r,t) = 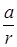cos(ωt – kr + a), (3.54)

где a— постоянная величина, численно равная амплитуде волны на расстоянии от источника, равном единице длины.

Найдем уравнение плоской волны, бегущей в трехмерном пространстве вдоль произвольного направления n. Выберем систему координат и возьмем волновую поверхность волны, находящуюся на расстоянии l от начала координат (рис.). Это будет плоскость, перпендикулярная вектору n. Если волна в начале координат задана уравнением:

u(0,t) = u₀×cos(ωt + a),

то колебания частиц на выбранной волновой поверхности будут иметь вид:

u(0,t) = u₀×cos(ωt –kl + a).

Из рис. видно, что 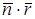= r×cosj = l , поэтому написанному выше уравнению можно придать вид:

u( 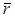,t) = u₀×cos(ωt - k× 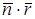+ a).

Введем вектор

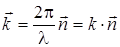, (3.55)

равный по величине волновому числу и направленный вдоль вектора n направления распространения волны. Величина 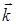называется волновым вектором. С его помощью уравнение плоской бегущей волны, распространяющейся в произвольном направлении n, приобретает вид:

u( 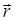,t)= u₀cos(ωt – 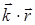+ a). (3.56)

Получим с помощью выражения (3.56) общий вид волнового уравнения, частным видом которого является (3.50). Колебания частиц в волне являются функцией четырех переменных — трех пространственных координат x, y, z и времени t. Продифференцируем выражение (3.56) по каждой из этих переменных дважды, пользуясь тем, что 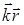= k_x+ k_y+ k_z:

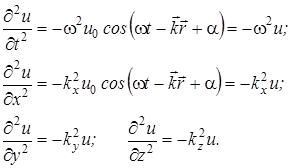
Складывая производные по координатам и выражая правую часть полученного выражения через производную по времени, находим:

.

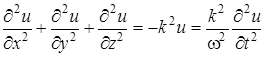Наконец, заменяя ω/k на фазовую скорость волны (3.52), окончательно получаем:

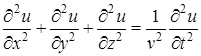. (3.57)

Это и есть общий вид волнового уравнения, который был выведен исходя из того, что выражение (3.51) представляет собой плоскую волну. На самом деле класс решений уравнения (3.57) необычайно широк. Всякая функция, котораяудовлетворяет уравнению(5.57), описывает какую-либо волну. Например, решением этого уравнения является и сферическая волна (3.54). Волны могут быть и более сложной формы.

Частным случаем уравнения (3.57) является одномерная волна (3.50) – в этом случае колебания в волне не зависят от остальных координат.