Колебания струны (стержня).

В натянутой струне, закрепленной с обоих концов, при возбуждении какого-либо произвольного поперечного возмущения возникнет довольно сложное нестационарное движение. Стационарное же движение в виде стоячей волны возможно лишь при вполне определенных частотах. Это связано с тем, что на закрепленных концах струны должны выполняться определенные граничные условия: в них смещение u все время должно равняться нулю. Значит, если в струне возбуждается стоячая волна, то концы струны должны быть ее узлами. Отсюда следует, что на длине струны l должно укладываться целое число п полуволн: l = n∙λ/2. Из этого условия находим возможные длины волн:

l_n = 2l/n, n = 1,2,...Соответствующие частоты ,

где v — фазовая скорость волны, определяемая, согласно (1.30), силой F натяжения струны и линейной плотностью ρ т. е. массой единицы ее длины.

Частоты ν_n называют собственными частотами струны. Частоту ν₁ (n=1) называют основной частотой, остальные ν₂, ν₃, ... — обертонами. Гармонические колебания с частотами (1.57) называют собственными колебаниями, или гармониками. В общем случае колебания струны представляют собой суперпозицию различных гармоник (спектр).

Колебания струны примечательны тем, что в рамках классической физики возникает дискретный спектр одной из величин (частоты). Такая дискретность для классической физики является исключением, в отличие от квантовой физики.

Приведенные выше соображения относятся не только к струне, но и к стержням, закрепленным различным образом — в середине, на одном конце и т. д. Отличие заключается лишь в том, что свободный конец стержня является пучностью. Это касается как поперечных, так и продольных колебаний.

Пример. Найдем собственные частоты стержня, закрепленного на одном конце, если длина стержня l, модуль Юнга материала стержня E и его плотность ρ.

Поскольку свободный конец стержня должен быть пучностью, на длине стержня установится целое число полуволн и еще четверть волны, т. е. l = nλ/2 + λ/4 = (2n + 1)λ/4. Отсюда найдем возможные значения λ_n, а затем, учитывая (1.26), и собственные частоты:

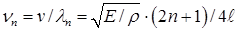, n=0,1,2,...