Уравнение состояния неидеального газа

Простая и удобная модель идеального газа применима в основном к разреженным газам, что соответствует малой плотности вещества. При больших давлениях и низких температурах возникают значительные отклонения от уравнения Клапейрона-Менделеева (2.8), что указывает на несоответствие модели идеального газа его реальному состоянию. Это означает, что уравнение состояния следует видоизменить, причем в его новом виде надо учесть отличие реальных молекул газа от модели невзаимодействующих материальных точек.

Прежде всего нужно учесть, что молекулы занимают вполне определенный объем в пространстве. Следовательно, область пространства, доступная для движения реальных частиц газа, не равна геометрическому объему, занимаемому газом, а меньше его на величину собственного объема молекул. Это обстоятельство легко учесть, если вместо геометрического объема теперь писать V ‑ b, где b — константа, характеризующая объем, занимаемый молекулами данного газа.

Далее необходимо заметить, что между реальными молекулами, имеющими сложную внутреннюю структуру, существуют силы взаимодействия. Эти силы имеют характер притяжения на сравнительно больших расстояниях и отталкивания на малых расстояниях. Вообще говоря, эти силы проявляются лишь при достаточном сближении молекул, поэтому в разреженных газах их можно не учитывать. Однако при низких температурах, когда энергия теплового движения молекул мала, и при больших давлениях, когда плотность газа возрастает, силы взаимодействия между молекулами начинают играть значительную роль. Макроскопически они проявляются в реальном газе как внутреннее давление, дополнительное к тому, которое обусловлено столкновениями молекул. Это дополнительное давление обусловлено взаимодействием молекул. Поскольку во взаимодействии принимают участие две группы молекул, число каждой из которых пропорционально плотности газа, то поправка к давлению пропорциональна квадрату плотности, то есть обратна пропорциональна второй степени геометрического объема, занимаемого газом. Таким образом, видоизмененное уравнение состояния принимает вид:

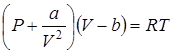, (2.45)

где a — другая константа, специфическая для данного газа и учитывающая характер сил взаимодействия между его молекулами. Уравнение (2.45) носит название уравнения Ван-дер-Ваальса. Когда объем газа становится достаточно большим, т. е., газ разрежен, поправками, связанными с отклонениями от идеальности, можно пренебречь и уравнение Ван-дер-Ваальса (2.45) переходит в уравнение Клапейрона-Менделеева(2.8).

Уравнение Ван-дер-Ваальса по сравнению с уравнением состояния идеального газа содержит ряд особенностей, отвечающих качественно новому поведению реального газа в области низких температур и больших плотностей. Как можно видеть из выражения (2.45), уравнение Ван-дер-Ваальса есть уравнение третьей степени относительно объема. Это означает, что при фиксированных температуре и давлении состояние газа может характеризоваться либо одним, либо тремя значениями V. На рис. изображены изотермы, соответствующие уравнению (2.45). При высоких температурах изотермы представляют собой кривые, характерные для идеального газа. При понижении температуры до определенной величины, которая называется критической, появляется характерный перегиб, ниже которого каждому значению давления отвечают три значения объема газа. Поэтому при данном давлении вещество может находиться в одном из трех возможных состояний или фаз. Состояние с минимальным объемом отвечает большей плотности вещества та. соответствует конденсации газа в жидкое состояние — жидкой фазе.

Состоянию с максимально возможным объемом отвечает газообразное состояние вещества. Промежуточное значение объема соответствует неустойчивому состоянию — его называют переохлажденный пар или перегретая жидкость. В этой области небольшие изменения давления вызывают немедленный переход вещества в одно из стабильных состояний. На рис. область существования неустойчивых состояний заштрихована. Она отделяет области существования жидкой и газообразной фаз вещества. Таким образом, важным следствием уравнения состояния неидеально газа является возможность фазового перехода вещества из одного состояния в другое. Кривые на диаграммах P,V или V,T, отделяющие области существования разных фаз, — это кривые фазового равновесия. Они показывают, при каких значениях параметров вещество может существовать в одном из состояний — твердом, жидком либо газообразном.

На рис. в координатах P, Т изображена, например, фазовая диаграмма для двуокиси углерода, на которой показаны области существования всех трех возможных фаз. Критическая температура для CO₂ равна 216,6 К, что составляет — 56,6 С. При обычных температурах и давлениях жидкая фаза не реализуется. В твердой фазе CO₂ представляет собой сухой лед. Он потому и называется сухой, что имеет низкую температуру, но не плавится, а сразу превращается в газовую фазу.