Скорость волны в тонком стержне.

Под тонким имеется в виду стержень, толщина которого мала по сравнению с длиной волны λ. При малых продольных деформациях стержня справедлив закон Гука:

s = E∙ε, (3.58)

где s = F/S — напряжение (Н/м2), E = kx/S — модуль Юнга (Па), ε = ¶u/¶x. Заметим, что s, как и ε, величина алгебраическая, и знаки s и ε всегда одинаковы: при растяжении — положительные, при сжатии — отрицательные.

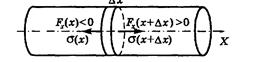
Рассмотрим малый элемент стержня Δx << λ в момент, когда при прохождении волны он оказался, например, в растянутом состоянии (рис.). Применим к этому элементу 2-й закон Ньютона:

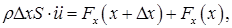
где ρ — плотность материала стержня, S — площадь его поперечного сечения. В данный момент, как видно из рисунка, Fx(x + Δx) > 0, a Fx(x) < 0. Соответствующие же значения s в сечениях x и x + Δx положительные (растяжение!). Поэтому правую часть уравнения можно переписать так:

,

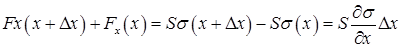где учтено, что слева Fx и s имеют разные знаки (это будет и при сжатии). Тогда уравнение движения после сокращения на Δx∙S примет вид

.

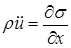Остается учесть (1.24), после чего получим окончательно:

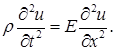
Мы пришли, таким образом, к волновому уравнению. Это позволяет утверждать, что в стержне будет распространяться продольная волна, скорость v которой легко определить:

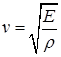
Заметим, что для не тонкого стержня выражение для v имеет более сложный вид и значение v оказывается больше, чем в случае тонкого стержня.