Мощность в цепи переменного тока

Мощность в цепи постоянного тока определяется произведением напряжения на силу тока:

P = UI.

Физический смысл этой формулы прост: работа А по перемеще­нию электрона из одной точки поля в другую равняется произведению заряда электрона на разность потенциалов U между этими точками,

А = Fd = еЕd = eUd/d = е U = IUt.

Произведение U∙I характеризует работу по перемещению заряда за единицу времени, протекающего через поперечное сечение проводника, т.е. является мощностью. Мощность электрического тока на данном участке цепи положительна, если энергия поступает к этому участку из остальной сети, и отрицательна, если энергия с этого участка возвращается в сеть. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока определяется такой же формулой:

P = UI.

Пусть напряжение на концах цепи меняется по гармоническому закону

U = U_mcos ωt,

(с тем же успехом, разумеется, вместо U = U_mcos ωt можно было бы записать U = U_mcos ωt), то и сила тока будет меняться со временем гармонически с той же частотой, но в общем случае будет сдвинута по фазе относительно напряжения:

I = I_mcos (ωt + φ_c),

где φ_c – сдвиг фаз между силой тока и напряжением. Поэтому для мгновенной мощности можно записать:

P = UI = U_mI_mcos ωt cos (ωt + φ_c) .

При этом мощность меняется со временем как по модулю, так и по знаку. В течение одной части периода энергия поступает к данному участку цепи

(р > 0), но в течение другой части периода некоторая доля энергии вновь возвращается в сеть (р < 0).

Чтобы найти среднюю мощность за период, воспользуемся известной формулой для произведения двух косинусов:

cos α cosβ = [cos(α – β) + cos(α + β)]/2 .

В рассматриваемом случае α = ω∙t и β = ω∙t + φ_c. Поэтому

P = U_mI_m/2[cos φ_c + cos(2ωt + φ_c)] = U_mI_m/2 cosφ_c + U_mI_m/2 cos(2ωt + φ_c).

Выражение для мгновенное мощности состоит из двух слагаемых. Первое не зависит от времени, а второе дважды за каждый период изменения напряжения изменяет знак: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течении другой части возвращается обратно. Поэтому среднее значение второго слагаемого за период равно нулю. Следовательно, средняя мощность p за период равна первому члену, не зависящему от времени:

P = U_mI_m/2 cosφ_c.

При совпадении фазы колебаний силы тока и напряжения (для активного сопротивления R) среднее значение мощности равно:

P = U_mI_m/2 = I²_mR/2.

Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = I∙U = I²∙R), вводятся понятия действующих значений силы тока и напряжения. Из равенства мощностей получим

P = I²_mR/2 = I²R или I²_m/2 = I², I = √ I²_m /√2 = I_m/√2.

Действующим значением силы I тока называют величину, в √2 раз меньшую ее амплитудного значения.

Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока.

Аналогично можно доказать, что действующее значение переменного напряжения в √2 раз меньше его амплитудного значения:

U = U_m/√2.

Заметим, что обычно электрическая аппаратура в цепях переменного тока показывает действующие значения измеряемых величин. Переходя к действующим значениям силы тока и напряжения, уравнение можно переписать:

P = U_m/√2 I_m/√2cosφ_c = UI cosφ_c.

Таким образом, мощность переменного тока на участке цепи определяется именно действующими значениями силы тока и напряжения. Она зависит также от сдвига фаз φ_c между напряжением и током. Множитель cos φ_c в формуле называется коэффициентом мощности.

В случае, когда φ_c = ± π/2 , энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор. Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рис. 10 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при φ_c = - π/2 (чисто индуктивное сопротивление участка цепи). График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть.

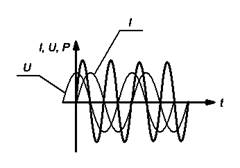
Рис. 10

Лишь при наличии проводника с активным сопротивлением в цепи, не содержащей движущихся проводников, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит.

При проектировании цепей переменного тока нужно добиваться, чтобы cos φ_c не был мал (φ_c должен быть близок к 0). Иначе значительная часть энергии будет циркулировать по проводам от генератора к потребителям и обратно. Так как провода обладают активным сопротивлением, то при этом энергия расходуется на нагревание проводов.

Неблагоприятные условия для потребления энергии возникают при включении в сеть электродвигателей, так как их обмотка имеет малое активное сопротивление и большую индуктивность. Для увеличения cos φ_c в сетях питания предприятий с большим числом электродвигателей включают специальные компенсирующие конденсаторы. Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой. Это уменьшает коэффициент мощности всей цепи. Повышение cos φ_c является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos φ_c < 0,85.