Среднеквадратическое значение сложных сигналов

Как уже говорилось, соотношение среднеквадратическое значение = 0,707 амплитуды справедливо только для синусоидальных сигналов. Среднеквадратиче­ское значение сигналов, имеющих другую форму, может быть определено следующим образом:

1. определяем квадрат площади положительной части сигнала за один период,

S²₊ = U²₊×t₊;

2. определяем квадрат площади отрицательной части сигнала за один период. Заметим, что при опре­делении площади отрицательное значение превращается в положи­тельное,

S²_- = U²_-×t_-;

3. определяем среднее значение суммарной площади сигнала за период

(S²₊ + S²_-) /T;

4. вычисляем квадратный корень из средней площади сигнала за период

U_д = √(S²₊ + S² _-) /T.

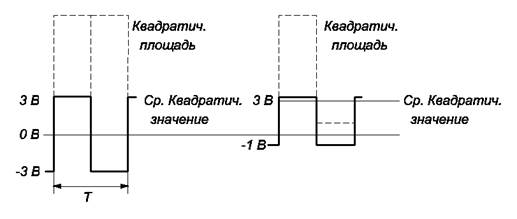
Рис.2.5

Определим среднеквадратическое значение сигнала, имеющего форму меандра (рис. 2.5):

1. площадь положительного полупериода составля­ет

S²₊ = 3²×T/2 = 9T/2;

2. площадь отрицательного полупериода составля­ет

S²_- = (-3)²×T/2 = 9T/2;

3. среднее значение площади за период, следователь­но равно

(S²₊ + S² _-) /T = (9×T/2 + 9×T/2)/T = 9T/T = 9;

4. среднеквадратическое значение напряжения будет равно

U_{д меан} = √9= 3 В.

Определим среднеквадратическое значение сигнала, имеющего не симметричную форму (рис. 2.6):

1. площадь положительного полупериода этого сигнала составля­ет

S²₊ = 3²×T/2 = 9T/2;

2. площадь отрицательного полупериода составля­ет

S²_- = (-1)²×T/2 = T/2;

3. среднее значение площади за период, следовательно, равно

(S²₊ + S² _-) /T = (9×T/2 + 1×T/2)/T = 10T/2T = 5;

4. среднеквадратическое значение напряжения будет равно

U_д = √5= 2,24 В.

Сравним среднеквадратическое значение синусои­дального напряжения имеющего значение положительной и отрицатель­ной амплитуды +3 В и -3 В, с среднеквадратическим значением сигнала, имеющего форму меандра.

U_{д sin} = 0, 707× 3 В = 2,12 В, U_{д меан} = √9= 3 В.

Как видим, прямоугольный сигнал имеет большее среднеквадратиче­ское значение. Это объясняется тем, что площадь под прямоугольной огибающей больше, чем площадь под синусоидой, хотя оба сигнала имеют одинаковые значения положительного и отрицательного пиков. В данном случае среднеквадратическое значение прямоугольного сигнала равно его пиковому значению.

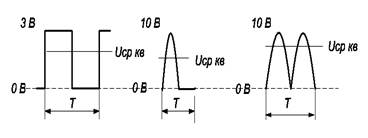
Рис. 2.6

На рис. 2.5 изображен прямоугольный сигнал, имеющий только по­ложительные значения. Определим среднеквадратическое значение сигнала, имеющий только по­ложительные значения (рис. 2.5):

1. площадь положительного полупериода этого сигнала равна

S²₊ = 3²×T/2 = 9T/2;

2. площадь отрицательного полупериода составля­ет

S²_- = (0)²×T/2 = 0;

3. среднее значение площади за период, следователь­но равно

(S²₊ + S² _-) /T = (9T/2 + 0)/T= 4,5;

4. среднеквадратическое значение напряжения будет равно

U_д = √4,5= 2,12 В.

Среднеквадратическое значение этого сигнала меньше его пикового значения.

Определим среднеквадратическое значение напряжения Sin сигнала, имеющий только по­ложительные значения (рис. 2.6):

1. площадь положительного полупериода этого сигнала равна

S²₊ = ₀∫^2πU²_мф sin² ωt dt = U_мф²× π/2 = 100× π/2

(предел интегрирования от – 0 до +2π);

2. площадь отрицательного полупериода составля­ет

S²_- = 0;

3. среднее значение площади за период, следователь­но равно

(S²₊ + S² _-) /T = (100× π/2+ 0)/2π= 100/4 = 25;

4. среднеквадратическое значение напряжения будет равно

U_д = √25= 5.

При однополупериодном выпрямлении среднеквадратическое значе­ние sin напряжения равно половине его амплитуды.

При двухполупериодном выпрямлении среднеквадратическое значе­ние такое же, как у полной синусоиды, т. е.,

U_д = 707 ×U_мф = 0,707× 10 = 7,07 В

поскольку при вычислении среднеквадратического значения отрицательный полу­период идентичен положительному.