Для одной материальной точки, движущейся в поле консервативных сил,

из (5.5)

A₁₂ = W_k2 - W_k1,

из (5.7)

A₁₂ = W_n1 - W_n2.

Откуда

W_n1 - W_n2 = W_k2 - W_k1

или

W_k1 + Wn1 = W_k2 + W_n2.

В поле консервативных сил сумма кинетической и потенциальной энергии материальной точки остается постоянной, т.е. сохраняется.

- полная энергия материальной точки.

Полная энергия материальной точки в поле консервативных сил сохраняется.

5.8.2. Полная энергия системы материальных точек
Для системы, состоящей из N взаимодействующих между собой материальных точек, полная энергия

,

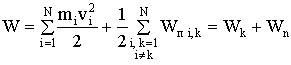где W_{п i, k} - потенциальная энергия взаимодействия i -й материальной точки с k-й материальной точкой.
W_п - потенциальная энергия взаимодействия всех частиц системы между собой.

5.8.2.1. Закон сохранения энергии для системы материальных точек
Если система материальных точек находится во внешнем поле консервативных сил, то её полная механическая энергия

,

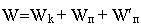где W'_п - потенциальная энергия системы во внешнем поле.
Полная механическая энергия системы материальных точек, находящейся только под действием консервативных сил, остается постоянной.
При наличии неконсервативных сил полная механическая энергия системы не сохраняется, ее убыль равна работе неконсервативных сил.