Кинетическая энергия. Помножим скалярно: слева на - справа на

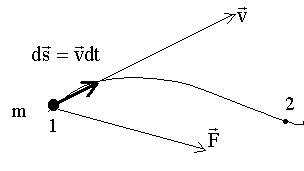
Применим II закон Ньютона для материальной точки m, движущейся под действием результирующей силы :

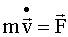
Помножим скалярно: слева на 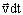- справа на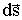

.

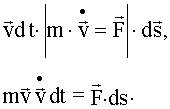Используя (5.3.2) справа и преобразуя левую часть,

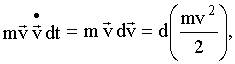
получим

.

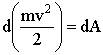Половина произведения массы частицы на квадрат ее скорости названа ее кинетической энергией

Таким образом элементарная работа, совершаемая над телом, равна элементарному приращению его кинетической энергии. При интегрировании вдоль траектории частицы, от точки 1 до точки 2, мы получим:

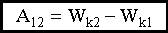
Работа результирующей силы идет на приращение кинетической энергии материальной точки.

5.6. Консервативные и неконсервативные силы
Консервативные (conservativus - охранительный) - такие силы, РАБОТА которых не зависит от траектории, а определяются только начальным и конечным положением материальной точки. Силы, не обладающие только что названным свойством, называют неконсервативными. Для того чтобы узнать, консервативна сила либо нет, надо вычислить ее работу.