Колебаний
Решение задач этого раздела рекомендуется выполнять в следующем порядке:
· выбрать систему отсчета, взяв начало координат в положении равновесия материальной точки;
· записать начальные условия движения материальной точки;
· составить дифференциальное уравнение движения материальной точки в проекции на соответствующую ось;
· проинтегрировать дифференциальное уравнение движения, использовав начальные условия движения для определения постоянных интегрирования.
·
При составлении дифференциального уравнения движения надо изобразить материальную точку в промежуточном положении, соответствующем ее положительной координате, предположив при этом, что точка перемещается в сторону возрастания этой координаты.
Пример 1.3.
Материальная точка колеблется по закону 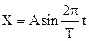 . При значениях координаты Х1 и Х2 ее скорость равна V1 и V2. Определить амплитуду и период колебаний.
. При значениях координаты Х1 и Х2 ее скорость равна V1 и V2. Определить амплитуду и период колебаний.
| A=?, T=? Х1 ,V1 Х2, V2 | 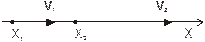
|
Решение
Найдем скорость колеблющейся материальной точки. По определению скорости имеем:
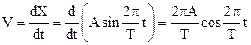 .
.
Используя данные задачи, образуем систему уравнений:
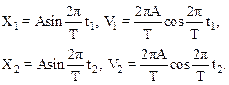
Выражая из полученных уравнений функции синуса и косинуса для моментов времени t1 и t2 и воспользовавшись тригонометрической единицей 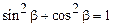 , получим:
, получим:
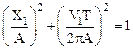 и
и 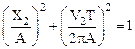 .
.
Решая систему, имеем:
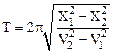 ,
, 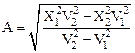
Дата добавления: 2015-08-08; просмотров: 754;
