Примеры решения задач по кинематике криволинейного движения
Пример 1.1. Снаряд вылетел под углом a = 300 к горизонту со скоростью V0 = 200 м/с. Определить скорость снаряда, а также его нормальное и тангенциальное ускорения через t = 3 с после начала движения. На какое расстояние S переместится за это время снаряд по горизонтали, на какой высоте он окажется?
Решение
| L=?, H=? аН=?, аt=?_________ V0=200 м/c, a=30°, g=9,8 м/с2 |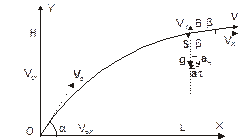 
|
Выберем двухмерную систему координат X,Y и совместим ее начало с положением снаряда перед выстрелом. Изобразим траекторию движения снаряда кривой ОВ и предположим, что снаряд через три секунды полета находится в точке В. Так как движение снаряда происходит с постоянным ускорением g, сообщаемым силой тяжести, и начальная скорость снаряда V0 не равна нулю, то законы кинематики должны быть записаны так:
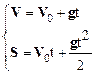, (1)
В проекциях на оси координат уравнения (1) имеют вид:
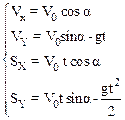
Величины V0cos α; и V0sin α равны проекциям начальной скорости на оси Х и Y, соответственно. Из ортогональности проекций Vx и Vy следует:
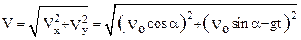(2)
Из чертежа видно, что проекции вектора перемещения S на оси координат равны горизонтальному L и вертикальному H перемещению снаряда: SX=L и SY=H, поэтому
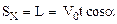(3)
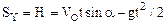(4)
Разлагая ускорение снаряда g в точке В на направления касательной и нормали к траектории, отметим его нормальную аН и тангенциальную аτ составляющие. Из чертежа видно, что
ан = g sinβ, ατ = g cosβ, (5)
β – угол между вертикалью и нормалью к траектории в точке В. В параллелограммах скоростей и ускорений имеются равные углы b (как углы с перпендикулярными сторонами).
Тригонометрические функции угла β можно найти из разложения скорости снаряда в точке В:
,
.
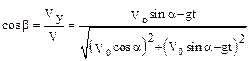Подставляя в соотношения (5) выражения для тригонометрических функций имеем окончательно:
,
.
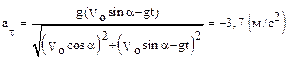Перемещение снаряда по горизонтали и его высоту находим по формулам (3) и (4):
, 
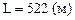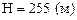, L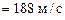 
.
С помощью соотношения (2) найдем величину скорости снаряда после трех секунд полета:
V=188 (м/c)
Замечание. Отрицательное значение ατ на третьей секунде полета показывает, что в этот момент скорость снаряда убывает, т. е. он еще находится на восходящей ветви параболы, например в точке В.
Пример 1.2. Диск радиусом R = 10 см находился в состоянии покоя, потом начал вращаться с постоянным угловым ускорением b=0,5 рад/с2. Найти тангенциальное, нормальное и полное ускорение точек на окружности диска в конце второй секунды после начала вращения, а также угол, который составляет вектор полного ускорения любой точки диска с его радиусом.
aH=?, at=?, а=?, a=?
R=10 см=0,1 м
b=0,5 с –2
t=2 c, w0=0
Решение
|
Разложим вектор полного ускоренияаточки на тангенциальное ускорение ατ и нормальное ускорение ан (n – вектор внешней нормали к траектории):
.
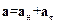Из рисунка видно, что tgα = ατ/αн. Используя связь линейных и угловых ускорений можно записать
ατ = βR.
Известно, что нормальное ускорение определяется формулой:
,
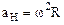где угловая скорость определяется из основного уравнения кинематики вращательного движения
.
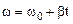По условию w0 = 0, тогда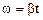 
.
Следовательно,
аН = β2 t2R.
Производя вычисления, получим:
ατ = 0.510-1= 5×10-2 (м/с2); ан = 25·10-2 · 4·10-2 =10-2 (м/с2).
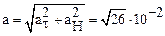(м/с2); 
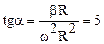, α =79°.
Дата добавления: 2015-08-08; просмотров: 1181;