Практическое занятие 2.

Теория

• Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением) .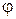

Кинематическое уравнение вращательного движения

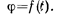
• Средняя угловая скорость

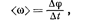
где 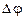— изменение угла поворота за интервал времени 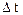. Мгновенная угловая скорость *

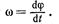
• Угловое ускорение *

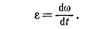
• Кинематическое уравнение равномерного вращения

где 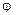—начальное угловое перемещение; t—время. При равномерном вращении 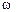=const и 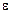=0.

*Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с осью вращения.

· частотота вращения

n=N/t, или n=1/T,

где N — число оборотов, совершаемых телом за время t; Т — период вращения (время одного полного оборота).

• Кинематическое уравнение равнопеременного вращения ( 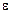= const.)

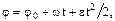
где 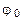—начальная угловая скорость; t—время.

Угловая скорость тела при равнопеременном вращении

.

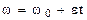• Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:

путь, пройденный точкой по дуге окружности радиусом R,

s= 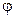R ( 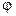— угол поворота тела);

скорость точки линейная

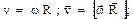
ускорение точки:

тангенциальное

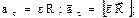
нормальное

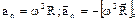
Пример 1. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R=50 м. Уравнение * движения автомобиля 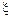(t)=A+Bt+Ct², где A=10 м, B=10 м/с, С=—0,5 м/с². Найти: 1) скорость v автомобиля, его тангенциальное 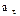, нормальное а_n. и полное а ускорения в момент времени t=5 с; 2) длину пути s и модуль перемещения | 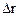| автомобиля за интервал времени 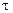=10 с, отсчитанный с момента начала движения.

Решение. 1. Зная уравнение движения, найдем скорость, взяв первую производную от координаты по времени:

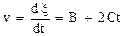. Подставим в это выражение значения В, С, t и произведем вычисления:

v=5 м/с.

Тангенциальное ускорение найдем, взяв первую производную от скорости по времени: 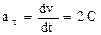Подставив значение С, получим 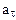= —1 м/с².

Нормальное ускорение определяется по формуле a_n=v²/R. Подставим сюда найденное значение скорости и заданное значение радиуса кривизны траектории и произведем вычисления:

a_n==0,5 м/с².

Полное ускорение, как это видно из рис. 1.1, является геометрической суммой ускорений а и а_n: а=а 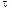+а_n. Модуль ускорения 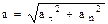. Подставив в это выражение найденные значения а и а_n получим

а=1,12 м/с².

2. Чтобы определить путь s, пройденный автомобилем, заметим, что в случае движения в одном направлении (как это имеет место в условиях данной задачи) длина пути s равна изменению криволинейной координаты 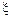т. е.

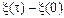s= , или .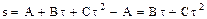

Подставим в полученное выражение значения В, С, 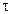и произведем вычисления:

s=50 м.

Модуль перемещения, как это видно из рис. 1.3, равен | 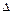r|=2Rsin( 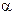/2),

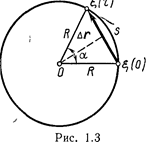
где 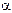— угол между радиусами-векторами, определяющими начальное 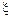(0) и конечное 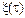положения автомашины на траектории. Этот угол (в радианах) находим как отношение длины пути s к радиусу кривизны R траектории, т. е. 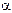= =s/R. Таким образом,

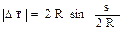
Подставим сюда значения R, s ипроизведем вычисления:

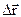| [= 47,9м.

Пример 4. Маховик, вращавшийся с постоянной частотой n₀=10 с¹, при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова стало равномерным, но уже с частотой п=6 с¹. Определить угловое ускорение 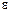маховика и продолжительность t торможения, если за время равнозамедленного движения маховик сделал N==50 оборотов.

Решение. Угловое ускорение маховика связано с начальной 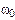и конечной 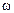угловыми скоростями соотношением 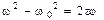, откуда 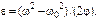Но так как 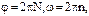то

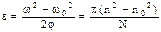
Подставив значения 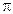, п, п₀, N и вычислив, получим

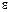=3,14(6²-10²)/50 рад/с²=—4,02 рад/с².

Знак минус указывает на то, что маховик вращался замедленно. Определим продолжительность торможения, используя формулу, связывающую угол поворота 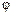со средней угловой скоростью <v> вращения и временем t: 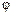=< 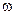>t. По условиям задачи, угловая скорость линейно зависит от времени и поэтому можно написать 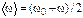, тогда ,

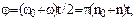Откуда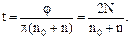

Подставив числовые значения и произведя вычисления, получим

Задачи

Криволинейное движение

1.26. Материальная точка движется по плоскости согласно уравнению r(t)=iAt³+jBt². Написать зависимости: 1) v(t); 2) a(t).

1.27. Движение материальной точки задано уравнением r(t)=A (icos 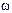t - j sin 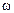t), где A =0,5 м, 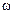=5 рад/с. Начертить траекторию точки. Определить модуль скорости |v| и модуль нормального ускорения |a_n|.

1.28. Движение материальной точки задано уравнением r(t)=i(A+Bt²)+jCt, где A==10 м, В= — 5 м/с², С=10 м/с. Начертить траекторию точки. Найти выражения v(t) и a(t). Для момента времени t=1 с вычислить: 1) модуль скорости |v| ; 2) модуль ускорения |а|; 3) модуль тангенциального ускорения |а 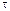|; 4) модуль нор­мального ускорения |a_n|.

1.29. Точка движется по кривой с постоянным тангенциальным ускорением a 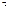=0,5 м/с². Определить полное ускорение а точки на участке кривой с радиусом кривизны R=3 м, если точка движется на этом участке со скоростью v==2 м/с.

1.30. Точка движется по окружности радиусом R==4 м. Начальная скорость v₀ точки равна 3 м/с, тангенциальное ускорение a 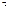=1 м/с². Для момента времени t=2 с определить: 1) длину пути s, пройденного точкой; 2) модуль перемещения | 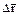|; 3) среднюю путевую скорость | 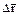|; 4) модуль вектора средней скорости |<v>|.

1.31. По окружности радиусом .R=5 м равномерно движется материальная точка со скоростью v=5 м/с. Построить графики зависимости длины пути s и модуля перемещения | 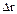| от времени t. В момент времени, принятый за начальный (t=0), s(0) и | 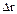(0)| считать равными нулю.

1.32. За время t=6 с точка прошла путь, равный половине длины окружности радиусом R==0,8 м. Определить среднюю путевую скорость <v> за это время и модуль вектора средней скорости |<v>|.

1.33. Движение точки по окружности радиусом R=4 м задано уравнением * 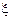=A+Bt+Ct², где A=10 м, В=—2 м/с, С=1 м/с². Найти тангенциальное а 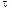, нормальное a_n и полное а ускорения точки в момент времени t=2с.

1.34. По дуге окружности радиусом R= 10 м движется точка. В некоторый момент времени нормальное ускорение точки а_n=4,9 м/с²; в этот момент векторы полного и нормального ускорений образуют угол 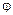=60°. Найти скорость v и тангенциальное ускорение a 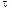точки.

1.35. Точка движется по окружности радиусом R=2 м согласно уравнению * 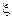=At³, где A =2 м/с³. В какой момент времени t нормальное ускорение а_n точки будет равно тангенциальному а 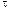.Определить полное ускорение а в этот момент.

1.36. Движение точки по кривой задано уравнениями x=A₁t³ и y=A₂t, где A₁==l м/с³, A₂=2 м/с. Найти уравнение траектории точки, ее скорость v и полное ускорение а в момент времени t=0,8 с.

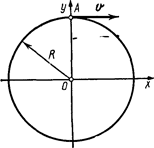
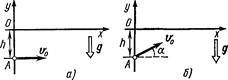
1.37. Точка А движется равномерно со скоростью v по окружности радиусом R. Начальное положение точки и направление движения указаны на рис. 1.8. Написать кинематическое уравнение движения проекции точки A на направление оси х.

1.38. Точка движется равномерно со скоростью v по окружности радиусом R и в момент времени, принятый за начальный (t=0), занимает положение, указанное на рис. 1.8. Написать кинематические уравнения движения точки: 1) в декартовой системе координат, расположив оси так, как это указано на рисунке; 2) в полярной системе координат (ось х считать полярной осью).

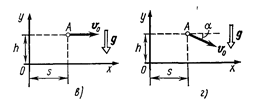
1.39. Написать для четырех случаев, представленных на рис. 1.9:

1) кинематические уравнения движения x=f₁(t) и x=f₂(t); 2) уравнение траектории у= 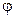(х). На каждой позиции рисунка — а, б, в, г — изображены координатные оси, указаны начальное положение точки A, ее начальная скорость v₀ и ускорение g.

1.40. С вышки бросили камень в горизонтальном направлении.

Через промежуток времени t=2 с камень упал на землю на расстоянии s=40 м от основания вышки. Определить начальную v₀ и конечную v скорости камня.

1.41. Тело, брошенное с башни в горизонтальном направлении со скоростью v=20 м/с, упало на землю на расстоянии s (от основания башни), вдвое большем высоты h башни. Найти высоту башни.

1.42. Пистолетная пуля пробила два вертикально закрепленных листа бумаги, расстояние l между которыми равно 30 м. Пробоина во втором листе оказалась на h=10см ниже, чем в первом. Определить скорость v пули, если к первому листу она подлетела, двигаясь горизонтально. Сопротивлением воздуха пренебречь.

1.43. Самолет, летевший на высоте h-=2940 м со скоростью v=360 км/ч, сбросил бомбу. За какое время t до прохождения над целью и на каком расстоянии s от нее должен самолет сбросить бомбу, чтобы попасть в цель? Сопротивлением воздуха пренебречь.

1.44. Тело брошено под некоторым углом 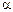к горизонту. Найти этот угол, если горизонтальная дальность s полета тела в четыре раза больше максимальной высоты Н траектории.

1.45. Миномет установлен под углом 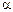=60° к горизонту на крыше здания, высота которого h=40 м. Начальная скорость v₀ мины равна 50 м/с. Требуется: 1) написать кинематические уравнения движения и уравнения траектории и начертить эту траекторию с соблюдением масштаба; 2) определить время 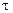полета мины, максимальную высоту Н ее подъема, горизонтальную дальность s полета, скорость v в момент падения мины на землю. Сопротивлением воздуха пренебречь.

Указание. Начало координат поместить на поверхности земли так, чтобы оно находилось на одной вертикали с минометом и чтобы вектор скорости vлежал в плоскости хОу.

1.46. Снаряд, выпущенный из орудия под углом 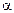=30° к горизонту, дважды был на одной и той же высоте h: спустя время t₁=10 с и t₂=50 с после выстрела.

Определить начальную скорость v₀ и высоту h.

1.47. Пуля пущена с начальной скоростью v₀=200 м/с под углом 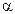=60° к горизонту. Определить максимальную высоту Н подъема, дальность s полета и радиус R кривизны траектории пули в ее наивысшей точке. Сопротивлением воздуха пренебречь.

1.48. Камень брошен с вышки в горизонтальном направлении с начальной скоростью v₀=30 м/с. Определить скорость v, тангенциальное a и нормальное a_n ускорения камня в конце второй секунды после начала движения.

1.49. Тело брошено под углом 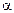=30° к горизонту. Найти тангенциальное a ; и нормальное а_n ускорения в начальный момент движения.

Рис. 1.8 Рис. 1.9

Вращение тела вокруг неподвижной оси

1.50. Определить линейную скорость v и центростремительное ускорение a_n точек, лежащих на земной поверхности: 1) на экваторе; 2) на широте Москвы ( 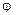=56°).

1.51. Линейная скорость v₁ точек на окружности вращающегося диска равна 3 м/с. Точки, расположенные на 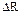=10 см ближе к оси, имеют линейную скорость v₂=2 м/с. Определить частоту вращения п диска.

1.52. Два бумажных диска насажены на общую горизонтальную ось так, что плоскости их параллельны и отстоят на d=30 см друг от друга. Диски вращаются с частотой n==25 с^-1. Пуля, летевшая параллельно оси на расстоянии r=12 см от нее, пробила оба диска. Пробоины в дисках смещены друг относительно друга на расстоя-ние s==5 см, считая по дуге окружности. Найти среднюю путевую скорость <v> пули в промежутке между дисками и оценить создаваемое силой тяжести смещение пробоин в вертикальном направлении. Сопротивление воздуха не учитывать.

1.53. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время t=3 с опустился на h= 1,5 м. Определить угловое ускорение 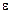цилиндра, если его радиус r=4 см.

1.54. Диск радиусом r=10 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением 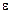=0,5 рад/с². Найти тангенциальное a 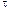, нормальное а_п и полное а ускорения точек на окружности диска в конце второй секунды после начала вращения.

1.55. Диск радиусом r=20 см вращается согласно уравнению 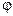=A+Bt+Сt³, где A=3 рад, В=—1 рад/с, С=0,1 рад/с³. Определить тангенциальное a 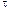нормальное а_n и полное а ускорения точек на окружности диска для момента времени t=10 с.

1.56. Маховик начал вращаться равноускоренно и за промежуток времени 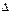t=10 с достиг частоты вращения n=300 мин"¹. Определить угловое ускорение 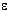маховика и число N оборотов, которое он сделал за это время.

1.57. Велосипедное колесо вращается с частотой п=5 с¹. Под действием сил трения оно остановилось через интервал времени 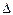t=1 мин. Определить угловое ускорение 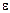и число N оборотов, которое сделает колесо за это время.

1.58. Колесо автомашины вращается равноускоренно. Сделав N=50 полных оборотов, оно изменило частоту вращения от n₁=4 с¹ до n₂==6 с¹. Определить угловое ускорение 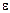колеса.

1.59. Диск вращается с угловым ускорением 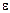=—2 рад/с². Сколько оборотов N сделает диск при изменении частоты вращения от n₁=240 мин ^-1 до n₂=90 мин ^-1? Найти время 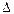t, в течение которого это произойдет.

1.60. Винт аэросаней вращается с частотой n=360 мин¹. Скорость v поступательного движения аэросаней равна 54 км/ч. С какой скоростью u движется один из концов винта, если радиус R винта равен 1 м?

1.61. На токарном станке протачивается вал диаметром d=60 мм. Продольная подача h резца равна 0,5 мм за один оборот. Какова скорость v резания, если за интервал времени t=1 мин протачивается участок вала длиной l=12 см?