Сила трения
Наряду с силами тяготения и упругими силами существуют силы, обусловленные молекулярными взаимодействиями между соприкасающимися поверхностями тел и зависящие от их скоростей. Опыт показывает, что сила трения, действующая на тело, направлена в сторону, противоположную его скорости. Поэтому работа сил трения всегда отрицательна:
dA=FTP·dr = FTP·v·dt = ‑FTP·v·dt = ‑FTP·dr. (1.65)
Следовательно, при наличии в системе сил трения полная механическая энергия системы уменьшается, переходя в другие формы энергии, а силы, приводящие к потере (диссипации) энергии, называются диссипативными. Таким образом, силы трения являются диссипативными силами. При наличии силы трения закон Ньютона приобретает вид:
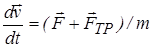 (1.66),
(1.66),
откуда
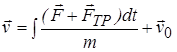 (1.67)
(1.67)
Если сила трения уравновешивает внешнюю силу, то тело будет двигаться равномерно и прямолинейно. Примером является свободное падение тела с учетом сопротивления воздуха, которое происходит с постоянной скоростью, зависящей от формы и размеров тела.
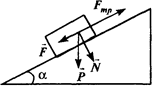
Рассмотрим трение скольжения (рис.). Силу тяжести Pможно разложить на две составляющие F и N, соответственно параллельно и перпендикулярно направлению скольжения. Сила N , прижимающая тело к поверхности, увеличивает взаимодействие между трущимися поверхностями. Сила трения скольжения противоположна направлению силы, заставляющей тело скользить. В то время как сила F = P sin a, сила трения
FTP = μ·N = μ·P·cosα. (1.68)
где μ — коэффициент трения, зависящий от формы и состояния соприкасающихся поверхностей, а также от скорости движения.
Механическая работа и мощность
Если на тело действует сила, то эта сила совершает работу по перемещению этого тела. Прежде чем дать определение работе при криволинейном движении материальной точки, рассмотрим частные случаи:
a)
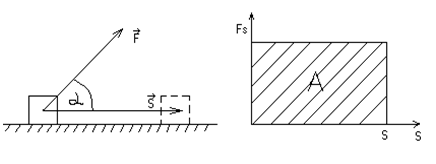 |
Сила постоянная
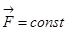 , движение прямолинейное.
, движение прямолинейное.
В этом случае механическая работа A равна:
A = F s cos 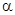 =
= 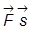 ,
,
или A = Fcos 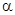 × s = FS × s ,
× s = FS × s ,
где FS – проекциясилы 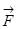 на перемещение. В данном случае Fs=const, и геометрический смысл работы A – это площадь прямоугольника, построенного в координатах FS, , s .
на перемещение. В данном случае Fs=const, и геометрический смысл работы A – это площадь прямоугольника, построенного в координатах FS, , s .
b) Движение прямолинейное, сила переменная, т.е. FS 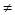 const.
const.
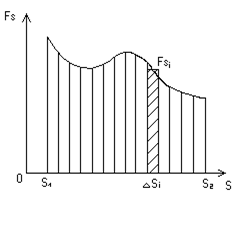
Построим график проекции силы на направление перемещения FS как функции перемещения s. Полное перемещение представим как сумму n малых перемещений  . Для малого i -ого перемещения
. Для малого i -ого перемещения  работа равна
работа равна 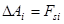
 или площади заштрихованной трапеции на рисунке.
или площади заштрихованной трапеции на рисунке.
 |
Полная механическая работа по перемещению из точки 1 в точку 2 будет равна:
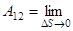
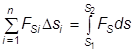 .
.
Величина, стоящая под интегралом будет представлять элементарную работу по бесконечно малому перемещению 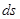 :
:
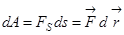 – элементарная работа.
– элементарная работа.
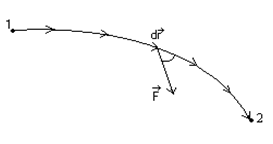
c) Движение криволинейное, сила 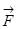 переменная.
переменная.
 Разбиваем траекторию движения материальной точки на бесконечно малые перемещения
Разбиваем траекторию движения материальной точки на бесконечно малые перемещения 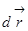 и работу силы
и работу силы 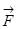 по перемещению материальной точки из точки 1 в точку 2 определяем как криволинейный интеграл:
по перемещению материальной точки из точки 1 в точку 2 определяем как криволинейный интеграл:
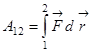 – работа при криволинейном движении.
– работа при криволинейном движении.
Пример 1: Работа силы тяжести 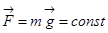 при криволинейном движении материальной точки.
при криволинейном движении материальной точки.
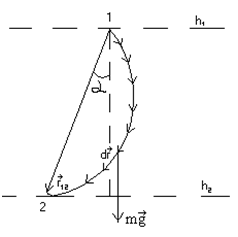
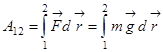 .
.
Далее 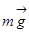 как постоянную величину можно вынести за знак интеграла, а интеграл
как постоянную величину можно вынести за знак интеграла, а интеграл 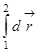 согласно рисунку будет представлять полное перемещение
согласно рисунку будет представлять полное перемещение 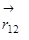 .
. 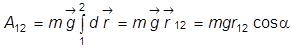 .
.
Если обозначить высоту точки 1 от поверхности Земли через 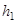 , а высоту точки 2 через
, а высоту точки 2 через 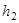 , то
, то
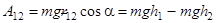 .
.
Мы видим, что в данном случае работа определяется положением материальной точки в начальный и конечный момент времени и не зависит от формы траектории или пути. Работа силы тяжести по замкнутому пути равна нулю: 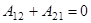 .
.
Силы, работа которых на замкнутом пути равна нулю, называетсяконсервативными.
Пример 2: Работа силы трения.
Это пример неконсервативной силы. Чтобы показать это достаточно рассмотреть элементарную работу силы трения:
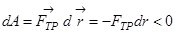 ,
,
т.е. работа силы трения всегда отрицательная величина и на замкнутом пути не может быть равной нулю. Работа, совершаемая в единицу времени, называется мощностью. Если за время 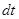 совершается работа
совершается работа 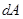 , то мощность равна
, то мощность равна
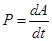 – механическая мощность.
– механическая мощность.
Взяв 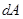 в виде
в виде
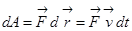 ,
,
получим для мощности выражение:
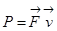 .
.
В СИ единицей работы является джоуль: 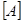 = 1 Дж = 1 Н
= 1 Дж = 1 Н  1 м, а единицей мощности является ватт: 1 Вт = 1 Дж/с.
1 м, а единицей мощности является ватт: 1 Вт = 1 Дж/с.
Механическая энергия.
Энергия является общей количественной мерой движения взаимодействия всех видов материи. Энергия не исчезает и не возникает из нечего: она лишь может переходить из одной формы в другую. Понятие энергии связывает воедино все явления в природе. В соответствии с различными формами движения материи рассматривают разные виды энергии – механическую, внутреннюю, электромагнитную, ядерную и др.
Понятия энергии и работы тесно связаны друг с другом. Известно, что работа совершается за счет запаса энергии и, наоборот, совершая работу, можно увеличить запас энергии в каком-либо устройстве. Другими словами работа – это количественная мера изменения энергии:
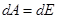 .
.
Энергия также как и работа в СИ измеряется в джоулях: [E]=1 Дж.
Механическая энергия бывает двух видов – кинетическая и потенциальная.
Кинетическая энергия(или энергия движения) определяется массами и скоростями рассматриваемых тел. Рассмотрим материальную точку, движущуюся под действием силы 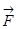 . Работа этой силы увеличивает кинетическую энергию материальной точки
. Работа этой силы увеличивает кинетическую энергию материальной точки 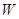 . Вычислим в этом случае малое приращение (дифференциал) кинетической энергии:
. Вычислим в этом случае малое приращение (дифференциал) кинетической энергии:
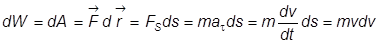 .
.
При вычислении 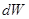 использован второй закон Ньютона
использован второй закон Ньютона 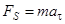 , а также
, а также 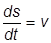 - модуль скорости материальной точки. Тогда
- модуль скорости материальной точки. Тогда 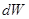 можно представить в виде:
можно представить в виде:
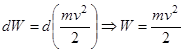 -
-
- кинетическая энергия движущейся материальной точки.
Умножив и разделив это выражение на 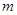 , и учитывая, что
, и учитывая, что 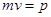 , получим
, получим
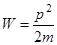 -
-
- связь между импульсом и кинетической энергией движущейся материальной точки.
Потенциальная энергия (или энергия положения тел) определяется действием на тело консервативных сил и зависит только от положения тела.
Мы видели, что работу силы тяжести 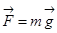 при криволинейном движении материальной точки
при криволинейном движении материальной точки 
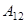 можно представить в виде разности значений функции
можно представить в виде разности значений функции 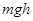 , взятых в точке 1 и в точке 2:
, взятых в точке 1 и в точке 2:
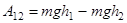 .
.
Оказывается, что всегда, когда силы консервативны, работу этих сил на пути 1  2 можно представить в виде:
2 можно представить в виде:
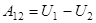 .
.
Функция 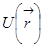 , которая зависит только от положения тела – называется потенциальной энергией.
, которая зависит только от положения тела – называется потенциальной энергией.
Тогда для элементарной работы получим
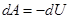 – работа равна убыли потенциальной энергии.
– работа равна убыли потенциальной энергии.
Иначе можно сказать, что работа совершается за счёт запаса потенциальной энергии.
Величину 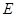 , равную сумме кинетической и потенциальной энергий частицы, называют полной механической энергией тела:
, равную сумме кинетической и потенциальной энергий частицы, называют полной механической энергией тела:
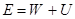 – полная механическая энергия тела.
– полная механическая энергия тела.
В заключении заметим, что используя второй закон Ньютона 
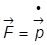 , дифференциал кинетической энергии
, дифференциал кинетической энергии 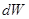 можно представить в виде:
можно представить в виде:
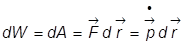 .
.
Дифференциал потенциальной энергии 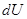 , как указывали выше, равен:
, как указывали выше, равен:
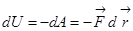 .
.
Таким образом, если сила 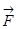 – консервативная сила и отсутствуют другие внешние силы, то
– консервативная сила и отсутствуют другие внешние силы, то 
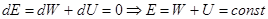 , т.е. в этом случае полная механическая энергия тела сохраняется.
, т.е. в этом случае полная механическая энергия тела сохраняется.
Закон сохранения механической энергии системы материальных точек.
Рассмотрим систему, состоящую из n материальных точек, между которыми действуют консервативные силы внутреннего взаимодействия 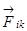 , и кроме того на материальные точки действуют внешние консервативные силы
, и кроме того на материальные точки действуют внешние консервативные силы 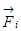 и внешние неконсервативные силы
и внешние неконсервативные силы 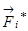 .
.
Для каждой материальной точки запишем второй закон Ньютона:
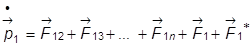 ,
,
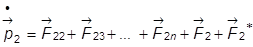 ,
,
– – – – – –
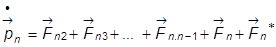 .
.
Далее левые и правые части каждого уравнения умножим скалярно на 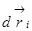 , соответственно, где
, соответственно, где 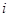 – номер материальной точки. Покажем это на примере
– номер материальной точки. Покажем это на примере 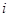 -ой материальной точки:
-ой материальной точки:
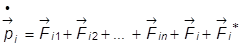 ½
½ 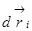 ,
,
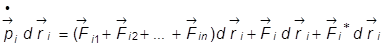 .
.
Это равенство можно записать в виде:
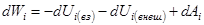 ,
,
или  ,
,
где 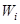 – кинетическая энергия
– кинетическая энергия 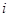 -ой материальной точки,
-ой материальной точки,
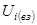 – внутренняя потенциальная энергия
– внутренняя потенциальная энергия 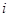 -ой материальной точки,
-ой материальной точки,
 – внешняя потенциальная энергия
– внешняя потенциальная энергия 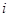 -ой материальной точки,
-ой материальной точки,
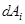 – работа, которую совершают над
– работа, которую совершают над 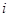 -ой материальной точкой внешняя неконсервативная сила.
-ой материальной точкой внешняя неконсервативная сила.
Просуммируем левые и правые части преобразованных указанным образом уравнений движения.
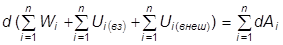 ,
,
или  ,
,
где 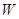 – кинетическая энергия системы материальных точек,
– кинетическая энергия системы материальных точек,
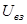 ,
, 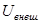 – внутренняя и внешняя потенциальная энергия м.т.,
– внутренняя и внешняя потенциальная энергия м.т.,
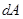 – полная работа внешних неконсервативных сил.
– полная работа внешних неконсервативных сил.
Если внешние неконсервативные силы отсутствуют, правая часть полученного уравнения будет равна нулю и, следовательно, полная механическая энергия системы остается постоянной:
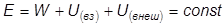 –
–
- закон сохранения механической энергии системы материальных точек.
Полная механическая энергия системы материальных точек, на которые действуют лишь консервативные силы, остается постоянной, т.е. сохраняется во времени.
Для замкнутой системы закон сохранения полной механической энергии имеет вид:
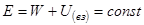 .
.
Полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остается постоянной, т.е. сохраняется во времени.
Если в замкнутой системе, кроме консервативных, действуют такие неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется.
Дата добавления: 2015-08-08; просмотров: 1982;
