Вопрос 3. Линейчатый спектр атома водорода

Важную роль в развитии планетарной модели атома сыграли эмпирические закономерности, полученные для линейчатого спектра атома водорода.

Иоганн Якоб Бальмер Иоганн Якоб Бальмер (1825-1898) Швейцарский физик и математик. Родился в Лозанне. Обнаружил закономерность в спектральных линиях атома водорода, показав (1885), что длины волн линий видимой части спектра атома водорода связаны между собой простой зависимостью (формула Бальмера), которая даёт возможность определить длины волн всех линий водородной серии (серия Бальмера). Это открытие послужило толчком для обнаружения других серий в спектре атома водорода - серий Лаймана, Пашена, Брэкетта и Пфунда. Первым начал изучение структуры атома.

В 1885г. швейцарский физик И. Бальмер (1825-1898гг.) установил, что частоты девяти линий в видимой области спектра водорода удовлетворяют соотношению:

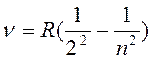(1)

(1) – формула Бальмера, где:

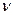- частота световой волны;

R - постоянная Ридберга ( );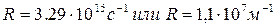

n – 3,4,5,…,11.

Все спектральные линии, удовлетворяющие соотношению (1) при любых целочисленных значениях 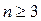, называются линиями серии Бальмера.

Максимальное значение частоты в серии Бальмера, получены при 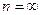, называется границей серии Бальмера.

В начале 20-го века в спектре водорода был обнаружен еще ряд спектральных линий, которые группируются в серии.

В УФ области спектра находится серия Лаймана:

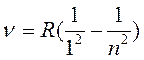(2)

m=2,3,…

В ИК области расположены еще 4 серии:

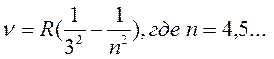- серия Пашена (3)

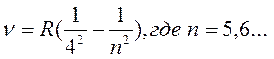- серия Брекетта (4)

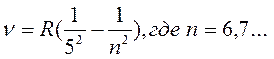- серия Пфунда (5)

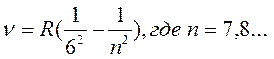- серия Хэмфри (6)

Все экспериментально найденные серии спектрах линий атома водорода могут быть описаны одной формулой:

– обобщенная формула Бальмера (7)

Для каждой серии число m принимает одно из 6-ти значений (1,2,…,6), a n пробегает весь бесконечный ряд целочисленных значений. Эмпирические формулы (1-6) неопровержимо указывали на особую роль целых чисел в спектральных закономерностях, которые, как оказались в дальнейшем, связаны с энергетическими уровнями атома водорода.