Логические основы построения ЭВМ

Для анализа и синтеза (создания) цифровых систем используется математический аппарат алгебры логики. Алгебра логики – это раздел математической логики, все элементы (функции и аргументы) которой могут принимать только два значения: 0 и 1.

Функция, однозначно определяющая соответствие каждой совокупности значений аргументов нулю или единице, называется функцией алгебры логики (ФАЛ). ФАЛ представляет собой алгебраическое выражение, содержащее переменные-аргументы, связанные между собой логическими операциями. Любая ФАЛ состоит из одной или более элементарных ФАЛ. Элементарной называется ФАЛ одного или двух аргументов, в логическом выражении которой содержится не более одной логической операции. Основные из элементарных ФАЛ приведены в табл. 3.2. Старшей является операция инверсии, более младшей – операция конъюнкции, самой младшей – операции типа дизъюнкции.

Технически ФАЛ реализуются специальными электрическими схемами, называемыми логическими элементами. Название и условное графическое обозначение (УГО) логических элементов также приведены в табл. 3.2. Логические элементы изготавливаются в виде интегральных микросхем, причем один корпус микросхемы содержит, как правило, несколько независимых однотипных логических элементов.

С целью упрощения устройств цифровых систем или применения в них однотипных логических элементов, соответствующие ФАЛ преобразовывают, используя при этом законы и тождества алгебры логики:

- сочетательный закон: aÙ(bÙс) = (аÙb) Ùс, аÚ(bÚс) = (аÚb)Úс,

а Å (b Å с) = (а Å b) Å с;

- переместительный закон: аÙb = bÙа, аÚb = bÚа, а Å b = b Å а;

- распределительный закон: аÙ(bÚс) = (аÙb)Ú(аÙс),

аÚ(bÙс) = (аÚb)Ù(аÚс), аÙ(bÅ с) = (аÙb)Å (аÙс);

- закон двойной инверсии: а = а;

- закон двойственности (правила де Моргана): аÚb = аÙb, аÙb = аÚb;

- закон поглощения: а Ú аÙс = а, aÙ(aÚc) = a;

- закон склеивания: аÙс Ú aÙc = a, (aÚс)Ù(aÚc) = a;

- тождества:

1) х Ú х = х, 4) х Ú х = 1, 7) х Ú 1 = 1, 10) х Ú 0 = х,

2) х Ù х = х, 5) х Ù х = 0, 8) х Ù 1 = х, 11) х Ù 0 = 0,

3) х Å х = 0, 6)х Å х = 1, 9) х Å 1 = х, 12) х Å 0 = х.

Здесь символ Ú обозначает операцию «дизъюнкция», символ Ù – операцию «конъюнкция», а символ Å – операцию «сумма по модулю два».

Таблица 3.2. Основные функции и операции алгебры логики и их

техническая реализация

Операция	Логический элемент	Правило выполнения операции	Функция
УГО	Название	a	b	y
Отрицание (инверсия)		НЕ (инвертор)				у =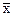
Дизъюнкция		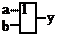ИЛИ				у = aÚb
Конъюнкция		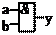И				у = aÙb
Стрелка Пирса		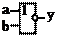ИЛИ-НЕ				у = a¯b = aÚb
Штрих Шеффера		И-НЕ				у = a | b = aÙb
Сумма по модулю 2		Исключающее ИЛИ				у = aÅ b = aÙb Ú aÙb
Равнозначность		Равнозначность				у = a∾b = aÅ b = aÙb Ú aÙb