Перевод из одной системы счисления в другую.
1. Для целой части используется правило последовательного деления
2. Для дробной части правило последовательного умножения.
Правило перевода целой части — правило последовательного деления: Для перевода целой части числа из С.С. с основанием p в С.С. с основанием q необходимо разделить целую часть заданного числа и получаемое частное на основание системы в которую необходимо преобразовать данное число, представленное в С.С. p, до тех пор пока частное не станет меньше q.
Старшей цифрой записи числа служит последнее частное, а следующие за ней дают остатки от деления частичных частных. Выписываются в порядке обратном их получения.
таким образом, получили число: (последнее частное) и затем остатки в порядке обратном их получения.
Двоичная система счисления Bin (Вinary)
Пример 4.Преобразовать десятичное число 134 в двоичное:
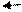 Частичные частные Частичные частные
| Последнее частное | ||||||||
| Остатки |
Получили число10000110 B
Правило перевода дробной части — правило последовательного умножения: Для перевода правильной дроби из С.С. с основанием p в С.С. с основанием q необходимо умножить исходную дробь и дробные части получающихся произведений на основание системы в которую необходимо преобразовать данное число, представленное в С.С. p. Целые части получающихся произведений дают последовательность цифр представления дроби в С.С. q.
Пример 5.Преобразовать десятичную дробь 0.375 в двоичную
0.375 * 2 = 0.75 0Старший Значащий Разряд (СЗР)
0.75 * 2 = 1.5 1
0.5 *2 = 1 1Младший ЗР (МЗР) Результат 0.011
Восьмеричная система счисления Oct (Оctal)
Восьмеричная система счисления имеет основание 8. В ней используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7. Восьмеричная система применяется для удобства записи чисел. Поскольку 23 = 8, то каждый восьмеричный символ (0 до 7) может быть представлен 3-х битовым числом (000 …..111)
Для перевода двоичного числа в восьмеричную систему счисления необходимо двоичное число разбить вправо и влево от запятой на триады (по три двоичных бита). При необходимости крайнюю левую триаду (целой части) и крайнюю правую (дробной части) дополняют нулями, затем каждую триаду заменяют восьмеричным числом.
Пример 6. Представить восьмеричным эквивалентом число:
10101011111101 ( B )=>25375 ( О )
| Двоичный код, разбитый на триады | 010 добавлен 0 | ||||
| Восьмеричный код |
Для перевода из восьмеричной в двоичную с.с. достаточно заменить каждую цифру восьмеричного числа соответствующим 3-х разрядным двоичным числом. При этом незначащие нули слева от целой части числа, и справа от дробной части отбрасываются.
Пример.7.Представить двоичным эквивалентом число:
375,75 ( O )=>11111101,1111 ( B )
| Восьмеричный код | 5, | ||||
| Двоичный | 101, |
Шестнадцатеричная система счисления Hex (Hexadecimal)
Используются символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. (А = 10, В = 11, С = 12, D = 13, Е = 14, F = 15)
Правило перевода шестнадцатеричных чисел в двоичные аналогично вышеизложенному, но используют не триады, а тетрады. Шестнадцатеричную цифру можно представить как средство сокращенной записи 4– х разрядного двоичного числа.
Преобразование двоичных чисел в 16-ные осуществляется по правилам, аналогичным для преобразования их в восьмеричные. Для этого биты целой и дробной частей влево и вправо от запятой группируются по четыре.
Пример 8. Представить шестнадцатеричным эквивалентом:
10101011111101 B => 25375 O => 2AFD H
| Двоичный код, разбитый на тетрады | ||||
| шестнадцатеричный код | А | F | D |
11000111.10101 B=>307.52 O => C7.A8 H
| Двоичный код, разбитый на тетрады | 1000 добавлены нули в конце дробной части | |||
| шестнадцатеричный код | С | A | ||
| Целая часть | Дробная часть |
Следует помнить, что 16-ные и 8-ные числа - это только способ представления двоичных чисел, которыми фактически оперирует микропроцессор.
Простота соотношения между 16 и 2 формами представления чисел – причина значительно большей распространенности 16 с.с.
Пример 9.Преобразование из двоичной системы в 8, 16, 101101.0111
B => 15.34O => D.7H
Пример 10.Преобразование из восьмеричной системы в 10, 16
1172.25 O => D; 634.328125 D => H,
ответ: 1172.25 O=>634.328125 D=>27A.54 H
Дата добавления: 2015-08-08; просмотров: 915;
