Закон Малюса. Пусть на поляризатор П падает линейно-поляризованный свет, плоскость поляризации которого составляет угол с плоскостью пропускания поляризатора (рис
Пусть на поляризатор П падает линейно-поляризованный свет, плоскость поляризации которого составляет угол  с плоскостью пропускания поляризатора
с плоскостью пропускания поляризатора 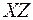 (рис. 66.1).
(рис. 66.1).
Разложим вектор 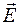 на две компоненты, одна из которых
на две компоненты, одна из которых 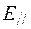 параллельна плоскости пропускания поляризатора, а другая
параллельна плоскости пропускания поляризатора, а другая 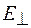 – перпендикулярна ей. Параллельная компонента
– перпендикулярна ей. Параллельная компонента 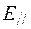 будет пропущена поляризатором, а перпендикулярная
будет пропущена поляризатором, а перпендикулярная 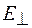 полностью поглотится. Тогда
полностью поглотится. Тогда  амплитуда напряженности электрического поля на выходе поляризатора
амплитуда напряженности электрического поля на выходе поляризатора 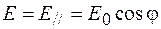 , где
, где 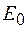 – амплитуда напряженности падающей волны. Интенсивность света пропорциональна квадрату амплитуды
– амплитуда напряженности падающей волны. Интенсивность света пропорциональна квадрату амплитуды 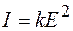 , где
, где 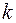 – коэффициент пропорциональности. Тогда для интенсивности прошедшего через поляризатор линейно-поляризованного света получим выражение
– коэффициент пропорциональности. Тогда для интенсивности прошедшего через поляризатор линейно-поляризованного света получим выражение
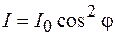 . (66.1)
. (66.1)
Соотношение (66.1) носит название закона Малюса.
Если на поляризатор направить естественный свет, у которого угол 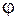 равномерно распределен в интервале от 0 до
равномерно распределен в интервале от 0 до  , то, усредняя (66.1) по углу
, то, усредняя (66.1) по углу 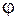 , получим
, получим
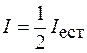 , (66.2)
, (66.2)
т. е. интенсивность естественного света  после прохождения через поляризатор уменьшается в два раза. При этом свет становится линейно-поляризованным.
после прохождения через поляризатор уменьшается в два раза. При этом свет становится линейно-поляризованным.
Если падающий на поляризатор свет представляет собой смесь естественного и линейно-поляризованного света, то при вращении поляризатора будет наблюдаться изменение интенсивности от максимального 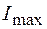 до минимального
до минимального 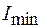 значений. Степенью поляризации света
значений. Степенью поляризации света 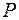 называется отношение
называется отношение
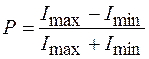 . (66.3)
. (66.3)
Для линейно-поляризованного света степень поляризации 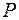 равна единице. Естественный свет имеет степень поляризации
равна единице. Естественный свет имеет степень поляризации 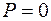 , а для частично поляризованного света
, а для частично поляризованного света 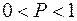 .
.
Дата добавления: 2015-08-08; просмотров: 1772;
