И электронных систем

Волновая оптика, фундаментом которой является электромагнитная теория Максвелла, сформировалась в XIX веке. До этого распространение света рассматривалось в рамках геометрической оптики. В середине XVII века французский ученый П. Ферма сформулировал основной принцип геометрической оптики (принцип Ферма): луч света, проходящий через две точки, идет между ними по такому пути, который требует наименьшего времени. Из этого принципа вытекают основные законы геометрической оптики – законы отражения и преломления.

Эти два закона позволяют рассчитать ход лучей в любой зеркально-линзовой системе, образованной совокупностью преломляющих и отражающих поверхностей. Например, если на тонкую сферическую линзу направить параллельный пучок лучей (рис. 64.1, а), то все лучи соберутся в одной точке 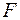, называемой фокусом линзы. То же самое произойдет, если вместо линзы использовать сферическое зеркало (рис. 64.1, б). Фокусирующее действие линз и зеркал используется в различных оптических приборах, таких как телескопы, микроскопы, проекционные системы и др.

Можно показать, что законы геометрической оптики вытекают из уравнений Максвелла при условии, когда длина волны , т. е. геометрическая оптика является предельным случаем волновой оптики, когда длиной волны можно пренебречь. В этом выражается принцип соответствия, согласно которому более общая теория должна включать результаты предшествующей теории в качестве предельного случая.

Поскольку геометрическая оптика не учитывает волновые эффекты, связанные с конечностью длины волны, то она дает лишь приблизительное описание распространения электромагнитных волн. Так, плоская волна, проходя через линзу, не будет фокусироваться в одной точке, как показано на рисунке 64.1. В результате дифракции на круглой оправе линзы в ее фокусе получится дифракционная картина, как на рисунке 56.1. В соответствии с формулой (56.1) радиус центрального светлого пятна (пятна Эйри)

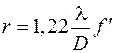, (64.1)

где 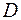– диаметр линзы; 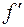– ее фокусное расстояние. Из выражения (64.2) видно, что точечное изображение ( 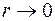) будет при условии, когда .

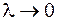Однако даже без учета дифракции изображение, формируемое оптической системой, будет отличаться от идеального. Искажения реального изображения по сравнению с идеальным называются аберрациями. Они определяются конструктивными параметрами оптической системы: радиусами кривизны, толщиной и коэффициентом преломления материала линз, взаимным расположением компонентов оптической схемы и другими параметрами. Различают волновую и геометрические аберрации. Волновая аберрация 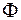характеризует отклонение реальной волновой поверхности от идеальной (рис. 64.2). Для точечного объекта идеальная волновая поверхность 1 представляет собой сферу, центр которой совпадает с изображением объекта. Реальная волновая поверхность 2 имеет более сложную форму. Волновую аберрацию выражают в длинах волн и обычно указывают максимальное или среднеквадратичное значение отклонения.

Так как реальная волновая поверхность для точечного объекта отличается от сферической, то изображение объекта имеет вид размытого пятна. Геометрические аберрации характеризуют размеры и форму этого пятна, и их делят на монохроматические и хроматические. К монохроматическим аберрациям относятся сферическая аберрация, кома, дисторсия, астигматизм и кривизна поля изображения.

Сферическая аберрация характеризует изображение точки, расположенной на оптической оси системы. Оно имеет вид круглого пятна, как изображено на рисунке 64.3, а. Расчеты показывают, что для сферической линзы параллельные лучи (рис. 64.1, а), идущие на разном расстоянии от оптической оси, пересекают ее в разных точках, поэтому в фокальной плоскости получается размытое пятно. Если точка смещена относительно оптической оси, то ее изображение имеет вид запятой, как показано на рисунке 64.3, б, и такая аберрация называется комой (от немецк. komma – запятая). Дисторсия характеризует различие увеличения оптической системы в разных точках плоскости изображения, вследствие чего изображение прямоугольного предмета (а) имеет подушкообразную (б) или бочкообразную (в) форму, представленные на рисунке 64.4. Кома и дисторсия зависят от положения точки в поле зрения оптической системы, поэтому их называют полевыми аберрациями.

Астигматизм характеризует неточечность (овальность) изображения, а кривизна поля изображения – отступление изображения от плоскости. Они также относятся к полевым аберрациям.

В реальной оптической системе присутствуют в той или иной степени все аберрации, однако путем подбора конструктивных параметров можно скомпенсировать отдельные аберрации, но никогда невозможно устранить их полностью. В телевидении, аэрофотосъемке (в том числе из космоса), астрономии и других областях науки и техники предъявляются высокие требования к качеству оптической системы, поэтому расчет высококачественной оптики представляет собой сложную инженерную задачу. В России (а ранее в Советском Союзе) накоплен большой опыт решения подобных задач, и отечественная оптика по праву считается одной из лучших в мире.

В телевизионной электронно-лучевой трубке (ЭЛТ) изображение формируется путем сканирования электронным пучком по внутренней поверхности экрана ЭЛТ, покрытого люминофором. Фокусировка электронного пучка на поверхности люминофора осуществляется с помощью электростатических или магнитных линз (электронной оптики). Электростатическая линза представляет собой металлический электрод Э специальной формы, который при подаче на него напряжения создает электрическое поле с заданной геометрией силовых линий (рис. 64.5). Электроны отклоняются полем, и пучок фокусируется на экране.

Расчет прохождения электронного пучка через электронные линзы аналогичен расчету хода лучей в оптической системе. Электронные линзы вносят аберрации так же, как и их оптические аналоги. Величина остаточных аберраций определяет качество телевизионного изображения.

Вопросы для самоконтроля

1. При каких условиях можно наблюдать интерференцию двух электромагнитных волн?

2. Поясните с помощью векторной диаграммы условия максимумов и минимумов интенсивности интерференционной картины.

3. Опишите различия в наблюдаемой интерференционной картине от двух точечных источников для двух случаев: а) частоты источников одинаковы; б) частоты источников немного отличаются.

4. Почему при отражении солнечного света от оконного стекла не возникает интерференционная картина?

5. При каких условиях наблюдается дифракция волн?

6. Сформулируйте условия наблюдения дифракции Фраунгофера и Френеля.

7. В чем заключается метод зон Френеля?

8. Опишите картины дифракции монохроматической волны а) на щели; б) на круглом отверстии; в) на крае полуплоскости; в) на дифракционной решетке.

9. Почему в картине дифракции монохроматической волны на дифракционной решетке выделяются главные максимумы?

10. Что такое угловая дисперсия и разрешающая способность дифракционной решетки? От чего они зависят?

11. Почему с помощью линзы невозможно получить точечное изображение бесконечно удаленного предмета?

12. Что общего и каковы различия бегущих и стоячих электромагнитных волн, получаемых от одного и того же источника.

Глава 6. ПОЛЯРИЗАЦИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН