ГИ сфокусированного изображения 5 страница

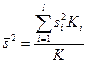, (16.4)

где 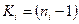- число степеней свободы; 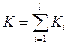, - число степеней свободы.

Далее на ходят В - критерий

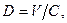(16.5)

здесь 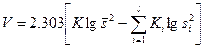, (16.6)

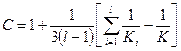. (16.7)

Бартлет установил, что если 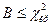, где 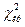- квантли распределения Пирсона, гипотеза о равенстве выборочных дисперсий может быть принята. Величина находится из табл. 2 приложения при 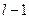степенях свободы и заданном коэффициенте риска 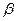. При 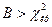признается значимость различия выборочных дисперсий .

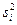Критерий Фишера ( 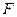-критерий). При анализе результатов эксперимента требуется не только уточнить вопрос о его воспроизводимости, оценивая однородность изменчивости и, в частности, дисперсии в различных опытах в ходе его проведения, но и оценить различие значений дисперсий для одной и той же случайной величины. Если эти различия являются случайными, то гипотеза о фактическом равенстве этих дисперсий является справедливой. В этом случае изменчивость, например, экспериментально полученных значений функции отклика, является ожидаемой для рассматриваемой генеральной совокупности их распределения.

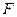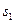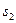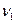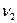При гауссовском законе распределения случайной величины для проверки гипотезы о равенстве двух дисперсий одной и той же случайной величины, в качестве критерия значимости используется -параметр, который равен отношению двух рассматриваемых выборочных дисперсий и , имеющих соответственно степени свободы и т. е.

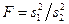. (16.8)

При расчете 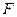-параметра по (16.8) должно выполняться условие . В противном случае следует поменять местами рассматриваемые дисперсии.

Найденное экспериментальное значение 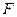-параметра сравнивается с его критическим значением 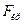, соответствующим максимальному значению отношения двух дисперсий, при котором еще можно считать гипотезу о равенстве рассматриваемых дисперсий справедливой.

Критичное значение 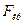по числу степеней свободы и заданному коэффициенту риска находится из табл. 5 приложения. Значение числа степеней свободы 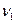дисперсии, стоящей в числителе выражения (16.8), определяет значение 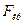по столбцу, а значение 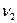- по строке. Если 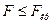, то гипотеза о равенстве выборочных дисперсий принимается. В противном случае, рассматриваемые дисперсии относятся к различным генеральным совокупностям исследуемой случайной величины.

Критерий Стьюдента ( 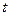-критерий). Для проверки гипотезы о равенстве двух выборочных средних значений случайной величины, имеющей гауссовский закон распределения, используется критерий Стьюдента. Для применения данного критерия подсчитывают выборочные средние арифметические значения случайной величины 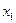и 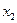, соответственно для выборок 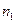и 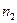и их выборочные стандартные отклонения

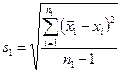и 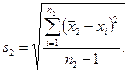(16.9)

Далее подсчитывают величину стандартного отклонения выборочных средних арифметических значений по формуле

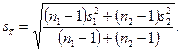
Для случая, когда среднее выборочное сравнивается с математическим ожиданием 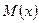генеральной совокупности 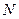, из которой берется выборка, и при условии, что 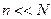, дисперсия средних подсчитывается по формуле

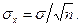(16.10)

Если генеральная характеристика 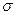неизвестна (а это наиболее часто встречающийся случай), то в (5.10) берется ее оценка

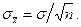
(16.11)

После того, как определены стандартные отклонения выборочных средних арифметических, подсчитывают размах Стьюдента:

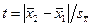или 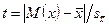. (5.12)

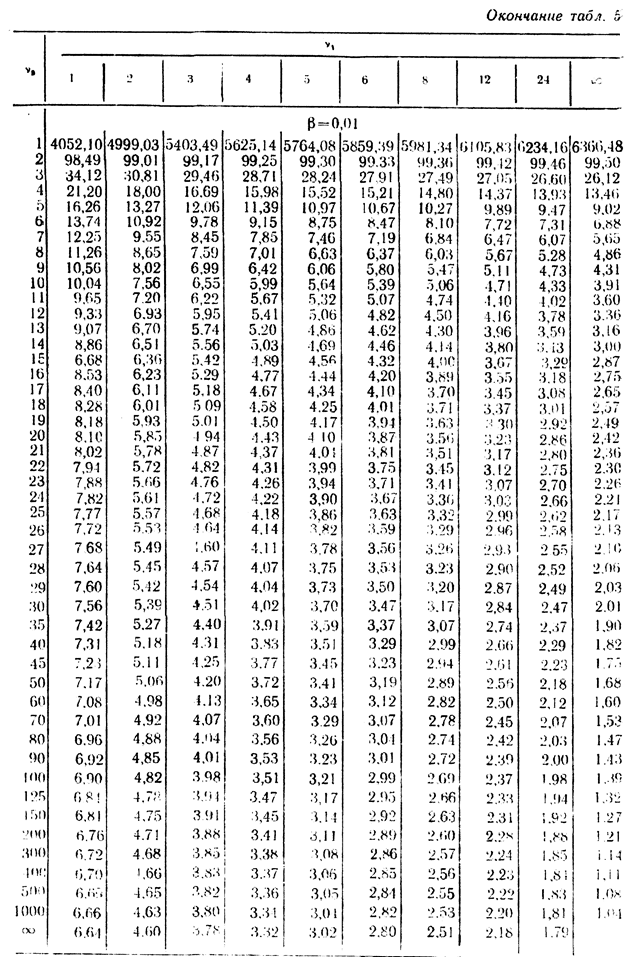
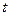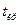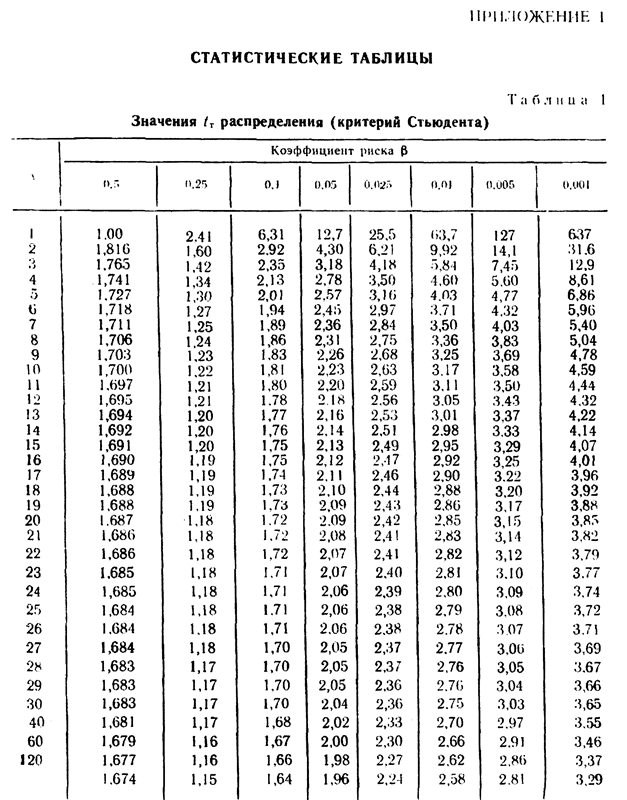
Найденное экспериментальное значение сравнивают с критичным значением , которое определяют по таблице распределения Стьюдента для заданного коэффициента риска 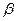(см. табл. 1 приложения) и числа степеней свободы .

______________________

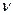1 Число степеней свободы - это разность между числом экспериментов и числом независимых случайных величин, полученных в результате этих экспериментов, которые не позволяют оцениваемой в результате этих экспериментов величине (например, среднему значению) принимать какое либо другое значение, отличное от полученного по окончании их проведения.

Если 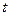≤ 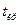, то гипотеза о равенстве выборочных средних арифметических значении принимается, а это значит, что выборки взяты из одной и той же генеральной совокупности.

При малом объеме выборки 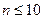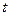- случайная величина и ее распределение не является гауссовским. Однако по мере увеличения объема выборки 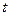- распределение приближается к гауссовскому. При его можно считать практически гауссоиским.

После вычисления коэффициентов имитационной модели, представленной в виде линейного полинома, оценивается их значимость для определения степени влияния различных факторов на выходной параметр (функцию отклика). Основой оценки значимости коэффициентов полинома является сопоставление абсолютного значения, например, коэффициента 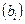и дисперсии ошибки его определения 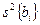. В этом случае с помощью 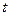-критерия проверяется гипотеза о незначимости рассматриваемого коэффициента, т. е. гипотеза о том, что 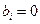(проверка нуль - гипотезы). Поэтому при подсчете экспериментального значения 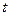-параметра, в отличие от (16.12), и числитель ставится абсолютное значение рассматриваемого коэффициента, а в знаменатель - дисперсия ошибки его определения, т. е. для оценки коэффициентов, стоящих в линейных членах полинома, имеем

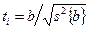. (16.13)

При ортогональном планировании эксперимента дисперсии ошибок определения каждого из коэффициентов равны между собой

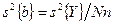, (16.14)

где 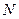- число номеров опытов определяющих в соответствии с матрицей планирования, условия проведения эксперимента; 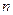- число параллельных опытов для каждого условия (номера опыта) проведения эксперимента.

Для оценки дисперсии воспроизводимости 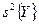можно воспользоваться группой выборочных дисперсий, приведенных в 14 столбце табл.14.1. Тогда

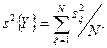(16.15)

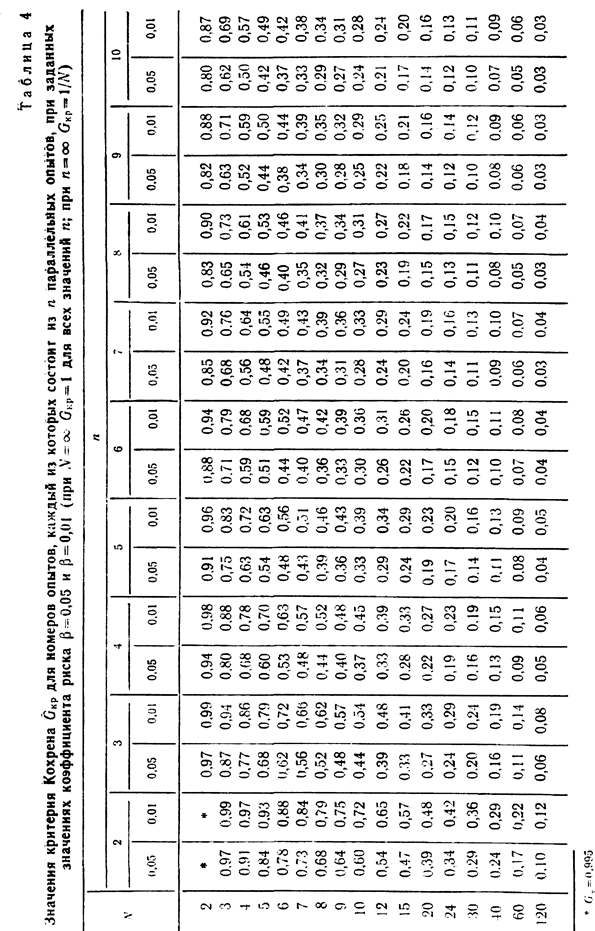
Коэффициент 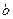признается незначимым, если 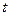для числа степеней свободы 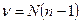меньше 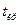, найденному из табл. 4 приложения для данного значения коэффициента риска .

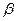Лекция 17

Порядок статистической обработки и анализ результатов эксперимента

Рассмотрим более подробно порядок статистической обработки и анализа результатов на примере ПФЭ. Следует отметить, что тот же самый порядок будет справедлив и при других методах планирования эксперимента, хотя расчетные формулы, разумеется, будут отличаться.

Обработка и анализ результатов ПФЭ предусматривает следующий порядок их проведения.

1. Оцениваются дисперсии среднего арифметическою в каждой строке матрицы по формуле

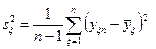. (17.1)

2. Проверяются однородности дисперсий. Так как даже одна грубая ошибка может исказить результаты исследования, проведенного при небольшом числе экспериментов, то необходим контроль воспроизводимости результатов исследования.

Если проверка показала, что эксперименты воспроизводимы, то их результаты можно использовать для оценки коэффициентов регрессии. Если же эксперименты невоспроизводимы, то неконтролируемые и неуправляемые факторы создают на выходе слишком большой уровень «шума». При отрицательном результате (эксперименты невоспроизводимы) проверяется следующая точка (имеющая второе по величине значение ) и т. д., т. е. выявляются все точки, в которых эксперимент невоспроизводим. При этом можно рекомендовать увеличить число параллельных опытов.

3. Создается математическая модель объекта с проверкой статистической значимости коэффициентов полинома.

После выполнения ПФЭ осуществляют независимую оценку

коэффициентов полинома по следующей формуле:

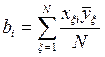, (17.2)

где 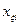принимает значения +1 или -1 в соответствии с матрицей планирования.

В числителе (17.2) фактически стоит сумма средних значений выходного параметра по всем опытам с учетом уровня независимой переменной 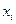в 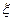-м опыте.

Следует отметить, что по формуле (17.2) мы можем найти также коэффициенты 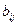при произведениях факторов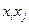 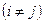. Значения этих коэффициентов показывают уровень влияния эффекта взаимодействия факторов 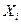и .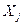

После вычисления коэффициентов оценивается их значимость для определения степени влияния различных факторов на выходной параметр. Основой оценки значимости является 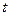- критерий (16.13).

Коэффициент 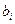признается незначимым, если 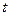для числа степеней свободы 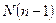меньше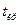 (см. табл. 1 приложения).

4. Провернется адекватность. Математическая модель должна достаточно верно качественно и количественно описывать свойства исследуемого явления, т. е. она должна быть адекватна. Это значит, что в некоторой подобласти, в которую входят и координаты выполненных опытов, предсказанное с помощью модели значение отклика не должно отличаться от фактического более чем на некоторую заранее заданную величину. Для проверки адекватности достаточно оценить отклонение предсказанного имитационной моделью значения выходного параметра 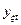от результатов эксперимента 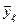в точке 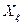факторного пространства.

Оцениваем дисперсию адекватности

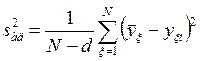, (17.3)

Где 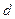- число членов аппроксимирующего полинома.

Если 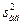не превышает дисперсии опыта 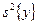, то полученная математическая модель адекватно представляет результаты эксперимента; если же 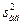> 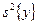, то проверка гипотезы об адекватности проводится с помощью 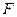-критерия пр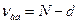и и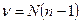

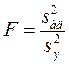(17.4)

если 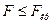, то модель признается адекватной.

Если полученная модель адекватна, то возможны следующие ситуации.

1. Все линейные коэффициенты значимы. Полученную модель можно использовать для управления процессом и оптимизации его путем движения в направлении к экстремуму.

2. Один из коэффициентов резко выделяется по абсолютной величине; в этом случае движение по градиенту функции выродится в обычный однофакторный эксперимент. Поэтому следует повторить эксперимент, уменьшив интервал варьирования этого фактора или увеличив его для других факторов.

3. Некоторые из линейных коэффициентов незначимы. Ими можно пренебречь, если соответствующие факторы действительно не оказывают влияния на выходной параметр (например, если незначимым оказался включенный в исследование из осторожности фактор, который и по априорным сведениям не должен оказывать существенного влияния па функцию отклика). Если в этом уверенности нет, то необходимо поставить новую серию опытов, расширив интервалы варьирования у соответствующих факторов.

4. Некоторые или все линейные коэффициенты незначимы, но значимы коэффициенты взаимодействия 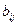. Такое положение может возникнуть из-за неудачного выбора интервалов варьирования, поэтому надо поставить новую серию опытов, увеличив интервалы варьирования у соответствующих факторов. Причиной подобной ситуации может быть и то, что эксперимент ставился и области, в которой линейное приближение является неудачной моделью поверхности отклика. В этом случае переходят к нахождению математической модели более высокого порядка.

Пример 1. В качестве примера обработки и анализа результатов эксперимента, рассмотрим пример 4, приведенный в лекц.14, и соответствующую ему матрицу планирования ПФЭ (табл.14.1).

1. Дисперсии опытных значении функции отклика около их средних значений в каждой строке матрицы приведены и столбце 14 табл.14.1. Наибольшее ее значение (0,08) соответствует условиям проведения эксперимента, установленным 1-м, 3-м и 6-м номерами опыта.

2. Для проверки воспроизводимости эксперимента подсчитаем по формуле (16.3) значение параметра :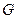

Критичное его значение, для 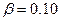, при (определяет 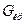по столбцу) и 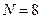(по строке), равно .

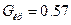Следовательно, эксперимент воспроизводим, так как согласно критерию Кохрена .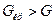

3. По (17.2) подсчитываем значение каждого коэффициента предполагаемой имитационной модели в виде полинома (13.2), на основании которой был спланирован и проведен эксперимент

;

.

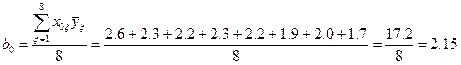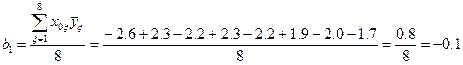Аналогично, подставляем в формулу (17.2) средние значения функции отклика и соответствующие им безразмерные значения факторов (или их взаимодействий), получаем:

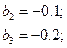
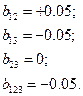
После вычисления коэффициентов предполагаемой модели исследуемого процесса, оцениваем их значимость с помощью критерия Стьюдента, предварительно рассчитав значение 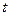- параметра по формуле (16.13) для каждого коэффициента и соответствующей ему дисперсии ошибки определения этого коэффициента. Учитывая ортогональность матрицы планирования ПФЭ, приведенной в табл.14.1 дисперсия ошибок каждого из коэффициентов будет одной и той же, определяемой по (16.14). Для вычисления дисперсии ошибки, предварительно нужно определить дисперсию воспроизводимости эксперимента (среднее значение всех оставшихся после проверки на воспроизводимость эксперимента дисперсий функции отклика в параллельных опытах – столбец 14 табл.14.1) по формуле (16.15):

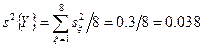
Тогда дисперсия ошибок определения коэффициентов полинома (13.2), в нашем случае, будет равна

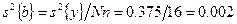
Теперь имеется возможность подсчитать 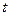-параметр для каждого коэффициента полинома (13.2):

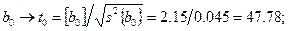
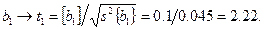
Подставляя в числитель выражения (16.13) абсолютное значение оцениваемого коэффициента, получаем соответствующее значение 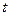-параметра:

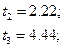
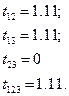
Определим критичное значение 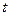-параметра по табл. 1 приложения 1 для 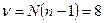и 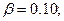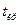=1,86.

Из сравнения найденного значения 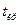с соответствующими значениями 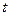- параметров, можно утверждать с уверенностью в нашей правоте в 9 случаях из 10, что коэффициенты 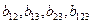являются незначительными. В этом случае эффектом взаимодействия учитываемых в эксперименте факторов можно пренебречь и уточненная имитационная модель, описывающая исследуемый процесс, примет вид:

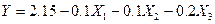. (17.5)

Из приведенной математической модели (17.5) видно, что самое большое влияние на функцию отклика 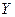оказывает третий фактор 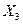(температура термообработки резистивных пленок), в то время, как увеличение двух других факторов в два раза меньше.

После уточнения вида имитационной модели необходимо проверить ее на адекватность исследуемому процессу. Учитывая, что аппроксимирующий полином (17.5) содержит четыре члена , дисперсия адекватности, в соответствии с (17.4), будет иметь следующий вид:

. (17.6)

Как видно из (17.6), для расчета дисперсии адекватности первоначально необходимо определить теоретические значения функции отклика 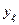, для каждого условия проведения опыта, соответствующего конкретному его номеру .

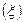Теоретические значения функции отклика определяются из (17.5) подстановкой безразмерных значений соответствующих факторов 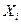, для каждого номера опыта.

Так, для условий эксперимента, соответствующих опыту №1, как видно из

табл. 14.1, значения факторов будут:

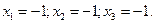
Тогда теоретическое значение функции отклика для этих условий проведения опыта, в соответствии с (17.5), будет равно

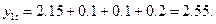
Аналогично, для последующих номеров опыта имеем

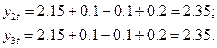
Рассчитанные таким образом теоретические значения функции отклика заносятся в столбец 15 табл.14.1, который примет следующий вид:

Номер опыта		Номер опыта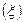
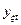
	2,55 2,35 2,35 2,15		2,15 1,95 1,95 1,95

Сравнивая теоретические значения 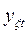функции отклика с ее экспериментальными средними значениями приведенными в столбце 13 табл.14.1, можно подсчитать дисперсию адекватности

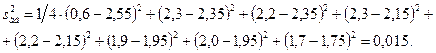
Таким образом, дисперсия адекватности 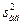меньше дисперсии воспроизводимости эксперимента 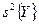, что свидетельствует об адекватности модели (17.5) исследуемому процессу, и она может быть использована для его оптимизации путем шагового движения к экстремуму. Если бы 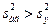, то следовало бы воспользоваться 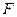- критерием.

СПИСОК ЛИТЕРАТУРЫ

1. Адлер Ю.П. и др. Планирование эксперимента при поиске оптимальных условий. М.: Наука. 1971. 283 с.

2. Блохин В.Г. и др. Современный эксперимент: подготовка, проведение, анализ результатов. Под ред. Грудкина О.П. М.: Радио и связь. 1997. 232 с.

3. Букеткин Б. В. И др.; Под ред. Вафина Р.К. Экспепиментальная механика. М.: Изд-во МВТУ им. Н.Э. Баумана. 2004. 136 с.

4. Венцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения. М.: Высш. шк., 2000. 480 с.

5. Венцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. М.: Высш. шк., 2000. 383 с.

6. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. Методы планирования эксперимента. М.: Мир, 1981. 520 с.

7. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. Методы обработки данных. М.: Мир, 1981. 610 с.

8. Сухарев И.П. Экспериментальные методы исследования деформаций и прочности. М.: Машиностроение.1987. 216 с.

9. Шенк Х. Теория инженерного эксперимента. М.: Мир. 1972. 382 с.