ГИ сфокусированного изображения 3 страница

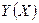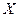При исследовании технологических процессов аналитическая зависимость (где - вектор управляемых, а значит, контролируемых факторов 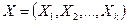) неизвестна и исследователь не может найти экстремум путем решения системы дифференциальных уравнений

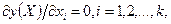(11.1)

где 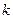- число факторов.

Обычно исследователь может лишь наблюдать значения выходной величины при различных комбинациях варьируемых факторов 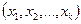; в действительности же наблюдается сумма истинного значения 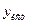и случайной ошибки опыта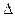

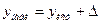. (11.2)

Принято называть геометрическое изображение функции отклика в факторном пространстве 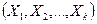— поверхностью отклика.

При поиске экстремальной точки, в отличие от аналитического исследования, осуществляется локальное изучение поверхности отклика по результатам ряда опытов, специально поставленных около исходной точки. Движение к экстремуму в 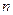- мерном пространстве независимых переменных осуществляется обычно не непрерывно, а шагами. Анализируя результаты экспериментов и сравнивая их с результатами предыдущих, исследователь принимает решение о дальнейших действиях по поиску оптимума. Экстремальное значение отклика достигается с помощью многократного последовательного изучения поверхности отклика и продвижения в факторном пространстве. Существуют несколько экспериментальных методов оптимизации, различающихся способом определения направления движения и организацией самого движения. Рассмотрим один из них.

Метод Гаусса —Зайделя. При оптимизации по этому методу последовательное продвижение к экстремуму осуществляется путем поочередного варьирования каждым фактором до достижения частого экстремума функции отклика (рис. 11.2). На рисунке изображены кривые равного выхода для одного из технологических процессов, аналогично кривым равной высоты на географических картах. Таким образом, изображающая точка перемещается попеременно вдоль каждой из координатных осей 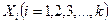факторного пространства; переход к новой 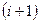- й координате осуществляется при достижении частного экстремума целевой функции 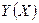по предыдущей координате, т. е. в точк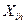е , где

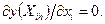(11.3)

Будем предполагать, что ищем экстремум в виде минимума функции отклика, максимум находится аналогично, меняется только знак.

Рис. 11.2. Поиск экстремума функции

отклика методом Гаусса - Зайделя

После достижения частного экстремума при изменении значений последнего фактора 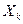, переходят снова к варьированию первым фактором и т. д.; в результате изображающая точка приближается к экстремуму. Направление движения вдоль 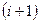- й координатной оси выбирается обычно по результатам двух пробных экспериментов в окрестностях точки частного экстремума по предыдущему фактору. Поиск экстремума прекращается в точке, движение из которой в любом направлении не приводит к уменьшению значения выходного параметра (функции отклика 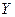). Точка поверхности отклика, в которой значение функции отклика будет минимальным, и будет искомым оптимумом. Точность определения оптимальной точки зависит от шага варьирования 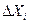, и, иногда, для увеличения точности уменьшают величину шага при приближении к экстремуму.

Важным моментом при постановке эксперимента является выбор исходной точки и шага варьирования. Здесь необходимо учитывать свойства изучаемого процесса, особенности технологии и методов измерения, т. е. привлекать всю априорную информацию об объекте исследования.

Лекция 12

Методы математической статистики в экспериментальных исследованиях

Основной целью проведения современного эксперимента с позиций производителя продукции является разработка математической модели, адекватно описывающей процесс и позволяющий в конечном результате, осуществлять его управление.

При планировании эксперимента исследователь должен:

1) обеспечить высокую надежность и четкость интерпретации результатов экспериментальных исследований;

2) составить четкую и последовательную логическую схему построения всего процесса исследования: что, когда и как нужно делать;

3) максимально формализовать процесс разработки модели и сопоставления экспериментальных данных различных опытов одного и того же объекта исследований с целью широкого применения электронно-вычислительных средств.

Всем перечисленным требованиям отвечают статистические методы планирования эксперимента, являющиеся одним из эмпирических способов получения математического описания сложных процессов. При применении статистических методов планирования эксперимента математическое описание процесса обычно представляется в виде полинома 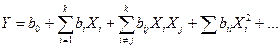, (12.1)

где 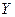- функция отклика, а 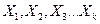— факторы исследуемого процесса.

План эксперимента в этом случае определяет расположение экспериментальных точек в 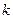- мерном факторном пространстве или, другими словами, условия для всех опытов, которые необходимо провести. Обычно план эксперимента задается в виде матрицы планирования, каждая строка которой определяет условия опыта, а каждый столбец - значения контролируемых и управляемых параметров в исследуемом процессе, т. е. значения факторов, соответствующих условию опыта.

В последний столбец матрицы заносят значения функции отклика 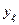, полученные экспериментальным путем в каждом 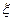- м опыте, проведенным в соответствии с условиями, указанными в строках матрицы планирования эксперимента.

Планирование эксперимента начинают с выбора центра плана, т. е. точки, соответствующей начальному значению всех используемых в эксперименте факторов 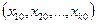, в окрестностях которой в дальнейшем ставится серия планируемых опытов. Очевидно, что начальным значениям факторов будет также соответствовать начальное значение функции отклика 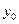. Центр плана

обычно выбирается на основе априорных сведений о процессе. Если же их нет, то обычно в качестве центра плана принимается центр исследуемой области.

Значение факторов в каждом опыте, в случае применения матрицы планирования эксперимента, отличается от начального их значения 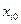на величину интервала варьирования 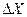. Одним из важнейших предварительных условий успешного проведения эксперимента с целью разработки математической модели, адекватной исследуемому процессу, является выбор оптимальной величины .

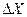Обычно интервал варьирования выбирают в пределах 0,05÷0,3 от диапазона варьирования исследуемого фактора. Далее, для удобства обработки результатов опытов, проводится преобразование значений управляемых переменных (учитываемых в эксперименте факторов 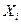) к безразмерным величинам

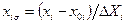, (12.2)

где 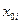— базовое или начальное значение 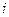-го фактора в центре плана; 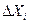- значение интервала варьирования по 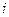- му фактору; 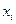- текущее значение 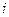-го фактора.

Пример 2. Предположим, что базовое значение температуры подложки – одного из факторов исследуемого процесса получения резистивных пленок (допустим 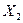), равно 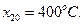При этом шаг варьирования по этому фактору 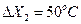. Варьирование значений фактора относительно его базового значения проводится на двух уровнях (рис. 12.1).

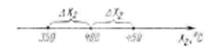Рис.12.1. Результаты пошагового варьирования фактора

Переходя от абсолютных значений рассматриваемого фактора к безразмерным его значениям, получим в соответствии с (4.1) для верхнего уровня рассматриваемого фактора 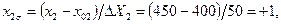а для нижнего -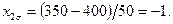

Таким образом, в безразмерной системе координат верхний уровень фактора при проведении эксперимента равен +1, а нижний -1. Координаты же центра плана равны нулю и совпадают с началом, координат. При составлении матрицы планирования эксперимента верхний и нижний уровни переменных для упрощения записи заменяют символом (+) и (-).

Разработку модели процесса следует проводить по принципу «от простого к более сложному». В соответствии с этим принципом, планирование эксперимента начинают с предположения, что имитируемая модель исследуемого процесса является линейной и в соответствии с (12.1) имеет вид полинома 1-го порядка

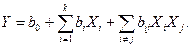(12.3)

Если после обработки и анализа результатов эксперимента выяснится, что сделанное предположение о линейности модели является ошибочным, переходят к планированию эксперимента из предположения, что эта модель может быть представлена полиномом 2-го порядка и т. д. до тех пор, пока не будет разработана адекватная исследуемому процессу математическая модель.

Рассмотрим наиболее распространенные статистические методы планирования экспериментов.

Лекция 13

Полный факторный эксперимент

В этом случае учитывается влияние на функцию отклика исследуемого процесса не только каждою рассматриваемого в эксперименте фактора в отдельности, но и их взаимодействий.

Под взаимодействием факторов понимают эффект влияния изменения значений одного или нескольких факторов на характер изменения функции отклика 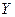от изменения другого фактора.

Примеры отсутствия и наличия взаимодействия факторов 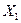и 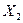приведены на рис. 13.1.

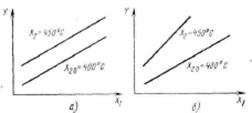
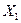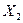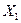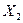Рис. 13.1. Примеры отсутствия взаимодействия факторов и (а) и наличия взаимодействия факторов и (б)

Влияние взаимодействия факторов — это когда уровень одного фактора определяет характер влияния другого фактора на выходной параметр. На рис. 13.1а переход второго фактора 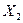с одного уровня 400° на другой 450° не меняет характер влияния первого фактор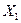а на 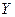; в этом случае взаимодействие факторов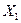 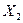не оказывает влияния на функцию отклика. На рис. 13.1б изменение уровня фактора 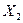сказывается на наклоне линейной зависимости 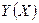, что говорит о влиянии взаимодействия факторов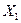 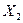на выходной параметр .

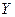При построении матрицы полного факторного эксперимента (ПФЭ), допустим, что в исследуемом процессе учитываются только два фактора 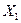и 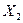оказывающие влияние на интересующую нас функцию отклика .

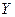В соответствии с принципом «от простого к более сложному» предположим, что модель исследуемого процесса является линейной и в соответствии с (11.3) имеет вид

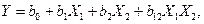(13.1)

где 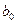- значение функции отклика 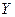в центре плана; коэффициент 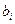, (в данном случае 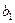и 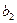) характеризуют степень влияния 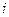-го фактора на функцию отклика 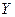(чем он больше по сравнению с другими коэффициентами, тем более весомый вклад в изменение 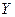данный фактор вносит); член 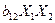учитывает эффект влияния взаимодействия 1-го и 2-го факторов на функцию отклика исследуемого процесса, а коэффициент 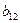характеризует весомость этого влияния.

Вполне очевидно, варьирование значений фактора относительно его базового (начального) значения в случае линейной модели достаточно проводить только на двух уровнях.

Очевидно так же, что все возможные комбинации для двух факторов ( 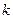=2), варьируемых на двух уровнях, будут исчерпаны, если мы поставим четыре опыта. Опытные точки расположатся в вершинах квадрата, центр которого совпадает с центром плана (рис. 13.2).

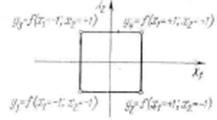
Рис.13.2. Расположение экспериментальных точек для двух независимых факторов, варьируемых на двух уровнях

Как видно, каждому из этих четырех опытов будет соответствовать свое значение функции отклика, в зависимости от четырех различных сочетаний 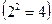двух значений варьируемых в данном эксперименте факторов.

Построим матрицу планирования ПФЭ для рассматриваемого случая, с учетом предполагаемой модели (13.1) исследуемого процесса.

При построении матрицы планирования ПФЭ существует следующее правило:

- первая строка матрицы в столбцах, соответствующих рассматриваемым в эксперименте факторам, заполняется безразмерным символом, соответствующим нижнему уровню значений фактора в эксперименте, т. е. символом (-); продолжение заполнения столбца, соответствующего первому по порядку фактору, проводится последовательным чередованием противоположных знаков (безразмерных значений уровней варьирования) все последующие столбцы, соответствующие другим пронумерованным по порядку факторам, заполняются с частотой смены знака вдвое меньшей, чем для предыдущего столбца.

Нумерация факторов осуществляется произвольно и в каждом конкретном случае определяется самим исследователем. Заполнение столбцов, учитывающих взаимодействие факторов, производится как результат перемножения знаков соответствующих факторов в каждой строке.

Первый столбец матрицы представляет собой нумерацию опытов. Во втором столбце матрицы планирования приводятся значения фиктивной переменной 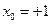, соответствующей коэффициенту 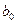. В последующих столбцах матрицы приводятся безразмерные символы, соответствующие верхнему и нижнему уровням варьирования факторов и их взаимодействий. В последний столбец матрицы заносятся экспериментальные значения функции отклика, полученные в результате проведения каждого опыта.

Матрица планирования ПФЭ, построенная в соответствии с этим правилом, приведена в таблице 13.1. Так как матрица построена для случая, когда в эксперименте рассматриваются только два фактора 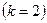, то ее называют матрицей планирования ПФЭ типа 2².

Таблица 13.1. Матрица планирования ПФЭ типа 2²

Номер опыта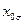
	+ + + -	- + - +	- - + +	+ - - +

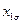
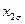
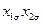
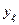
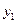
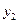
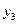
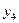
При обработке и анализе результатов эксперимента необходимо оценивать коэффициенты предполагаемой математической модели, представленной в нашем случае в виде полинома (13.1).

Для обеспечения независимости оценки коэффициентов полинома необходимо соблюдение независимости столбцов матрицы планирования эксперимента, или, говоря по-другому, построенная матрица планирования должна быть ортогональной.

Матрица планирования эксперимента является ортогональной, если сумма произведений значений, приведенных в каждой строке двух любых столбцов матрицы, соответствующих рассматриваемым в эксперименте факторам или их взаимодействию, равна нулю.

Пример 3. Проверим матрицу, приведенную в табл.13.1, на условие ортогональности (см. таблички).

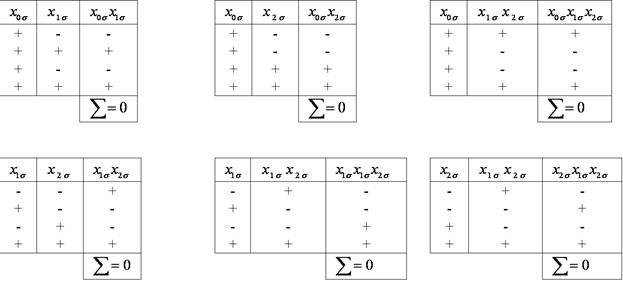
Проверка матрицы, приведенной в табл. 13.1, показала, что она является ортогональной, следовательно, с ее помощью можно производить независимую оценку коэффициентов полинома, так как соответствующие столбцы — независимы.

Если в эксперименте используются три фактора, а предполагаемая математическая модель линейна, то она соответствует полиному вида

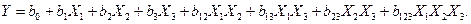(13.2)

При варьировании каждым из трех факторов 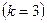на двух уровнях число опытов 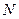будет составлять 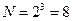, а матрица планирования ПФЭ будет иметь следующий вид (табл.13.2).

Таблица 13.2 Матрица планирования ПФЭ типа 2³

Номер опыта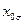
	+	-	-	-	+	+	+	-
	+	+	-	-	-	-	+	+
	+	-	+	-	-	+	-	+
	+	+	+	-	+	-	-	-
	+	-	-	+	+	-	-	+
	+	+	-	+	-	+	-	-
	+	-	+	+	-	-	+	-
	+	+	+	+	+	+	+	+

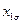
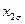
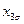
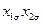
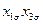
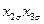
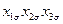
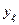
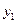
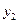
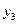
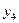
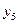
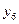
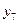
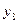
В этом случае опытные точки располагаются в вершинах куба, центр которого находится в начале координат (0, 0, 0) (рис.13.3).

Рис.4.6. Расположение экспериментальных точек в плане, соответствующем полиному

2-го порядка для трех независимых переменных

Руководствуясь приведенным ранее правилом, легко построить матрицу и для большего числа рассматриваемых в эксперименте факторов, число опытов в которой

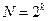, (13.3)

где 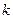— число учитываемых в эксперименте факторов.

Однако следует подчеркнуть, что выражение (13.3) справедливо только для линейной модели, соответствующей полиному 1-го порядка (11.3), когда варьирование по каждому фактору достаточно проводить на двух уровнях.

При статистическом методе планирования эксперимента существует правило - число уровней варьирования, учитываемых в эксперименте факторов, должно быть, по крайней мере, на единицу больше порядка полинома, для построения которого планируется эксперимент. Нами рассматривалось планирование эксперимента исходя из предположения, что математическая мотель исследуемого процесса соответствует полиному 1-го порядка (линейна). Поэтому достаточно было проводить варьирование каждого из 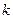факторов только на двух уровнях, а необходимое число проводимых опытов можно было определить с помощью выражения (13.3).

Если анализ результатов эксперимента показывает, что линейная модель, соответствующая полиному первого порядка (11.3) не адекватна исследуемому процессу, то переходят к планированию и проведению следующего эксперимента исходя уже из предположения, что математическая модель соответствует полиному следующего порядка и т. д. Но при планировании эксперимента, основанного на математической модели, например, соответствующей полиному 2-го порядка

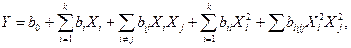(13.4)

необходимо обеспечить варьирование по каждому из 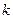факторов уже на трех уровнях. А тогда необходимое число опытов, которое нужно провести в эксперименте, должно быть не меньше Для полинома третьего порядка 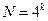и т. д.

Отметим некоторые положительные особенности многофакторного планирования ПФЭ.

1. Опытные точки находятся в оптимальном положении, т. е. математическое описание исследуемого процесса оказывается более точным, чем при проведении опытов в точках, расположенных каким-либо другим образом.

Поясним это утверждение. Если мы проводим эксперимент с небольшим интервалом 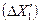варьирования (рис.13.4), то из-за наличия ошибки эксперимента, которая всегда имеется, положение искомой зависимости 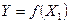будет определена с разбросом (I) значительно большим, чем при увеличенном 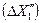интервале варьирования (II). В многофакторном эксперименте (ПФЭ) расстояние между экспериментальными точками без увеличения интервала варьирования по каждой переменной увеличивается в

Рис.13.4. Влияние размера интервала варьирования на точность

определения зависимости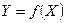

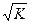раз (где 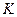- число факторов) по сравнению с однофакторным экспериментом. Так, для двухфакторного эксперимента (рис.13.2) – расстояние между экспериментальными точками – диагональ квадрата 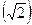, для трехфакторного эксперимента – диагональ куба 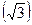и т.д.

2. Планирование и проведение ПФЭ сравнительно просто, что объясняет его широкое применение в практике.