ГИ сфокусированного изображения 4 страница

3. Все факторы и соответственно коэффициенты полинома оцениваются независимо друг от друга, что обеспечивается независимостью и ортогональностью столбцов матрицы планирования.

Однако последняя положительная особенность ПФЭ справедлива только для процесса, описываемого полиномом 1-го порядка. При значительном влиянии на выходной параметр уже квадратичных членов полинома, оценить раздельно коэффициенты 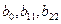и т.д. с помощью ПФЭ, как правило, не удается, так как соответствующие столбцы матрицы планирования будут идентичны между собой, и, матрица становится неортогональной, т.е. с зависимыми столбцами.

Лекция 14

Проведение эксперимента

Проведение эксперимента должно обеспечить сведение к минимуму влияние случайных параметров исследуемого процесса. Для достижения этой цели необходимо придерживаться следующих требований:

- предусмотреть проведение нескольких параллельных опытов при одних и тех же условиях, предусмотренных соответствующей строкой матрицы планирования (номером опыта);

- необходимо рандомизировать неконтролируемые параметры процесса, т.е. обеспечить их взаимную компенсацию.

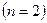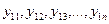Для выполнения первого требования должно быть предусмотрено проведение не менее двух параллельных опытов , а для более высокой достоверности результатов, их число увеличивают. В этом случае результаты параллельных опытов, например, для первой строки матрицы табл. 13.2, усредняются и при анализе результатов эксперимента используют именно усредненное значение функции отклика, соответствующее условиям опыта и подсчитываемое по формуле

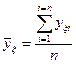. (14.1)

где 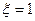, 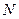- номер опыта по порядку, установленному первым столбцом матрицы, а 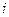- номер параллельного опыта в ее строке; 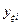значение функции отклика, соответствующее 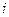-му параллельному опыту в 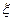-м номере опыта; 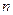- число параллельных опытов.

Для выполнения второго требования порядок реализации условий опыта, предусмотренный первым столбцом матрицы, должен быть рандомизирован. Для этого перед непосредственной реализацией плана эксперимента для каждой из 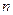серий опытов обычно с помощью таблицы случайных чисел определяется последовательность опытов на исследуемом объекте.

Пример 4. Требуется исследовать процесс получения резистивных пленок с целью его оптимизации. Напомним предварительные условия эксперимента. В качестве критерия оптимизации берется температурный коэффициент сопротивления (ТКС) Задача исследования - определить условия получения резистивных пленок с минимальным ТКС. Из анализа технологического процесса и результатов предварительных опытов установлено, что на ТКС пленок оказывают влияние следующие факторы: температура испарения материала (фактор 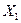); температура подложки, на которую производится осаждение материала (фактор 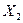); температура термообработки изготовленных резистивных пленок (фактор 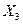). С учетом результатов предварительных опытов выбираем: центр плана 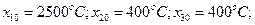шаг варьирования по всем трем факторам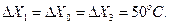

Абсолютные значения верхнего и нижнего уровней, учитываемых в данном эксперименте факторов приведены ниже.

Характеристика фактора	Значение фактора
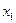
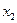
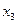
Верхний уровень 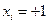Нижний уровень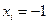

Предположим, что искомая модель исследуемою процесса является линейной и может быть представлена полиномом 1-го порядка вида (13.2). В этом случае достаточно варьирования каждою из трех факторов 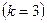на двух уровнях минимальное число опытов .

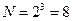С целью ускорения проводимого эксперимента, принимаем решение о проведении двух параллельных опытов 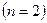для одних и тех же условий, представленных в каждой строке (значения верхнего и нижнего уровней факторов), соответствующих номеру опыта, указанному в 1-м столбце матрицы. С учетом проведения параллельных опытов, их число увеличивается до 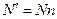и в нашем случае составит 16.

План эксперимента представим в виде матрицы планирования ПФЭ типа 2³ (табл.14.1), которая несколько отличается от матрицы, представленной в табл. 13.2.

Во 2-м столбце матрицы табл. 14.1 указан порядок проведения опытов, номера которых указаны в 1-м столбце матрицы и которым соответствуют условия, приведенные в 4, 5 и 6 столбцах матрицы.

Для рандомизации неконтролируемых параметров исследуемого процесса порядок проведения опытов определен с помощью таблицы случайных чисел. Так, в соответствии с порядком, указанном во втором столбце табл.14.1, первым проводится опыт, соответствующий третьему номеру опыта, указанному в первом столбце (третьей стоке плана), затем седьмой и т. д. Точно также во второй серии параллельных опытов порядок их проведения определен второй колонкой 2-го столбца матрицы планирования.

Все экспериментально полученные значения функции отклика первого и повторного опытов заносятся в 11 и 12 столбцы матрицы, а их средние значения подсчитываются по (14.1) и затем заносятся в 13 столбец.

Для проведения последующего анализа результатов эксперимента в матрицу планирования, представленную в табл.14.1, вводятся дополнительно 14 и 15 столбцы. При этом в 14 столбец вносятся значения выборочных дисперсий экспериментальных значений функции отклика 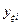около их среднего значения 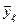, подсчитываемого по формуле

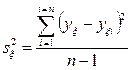. (14.2)

где 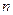- количество значений 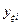, полученных в результате проведения 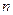параллельных опытов; .

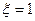Последний (15) столбец матрицы включает теоретические (буква 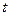является первой буквой слова theoretical - теоретическое) значения функции отклика 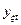, подсчитанные из предполагаемой имитационной модели исследуемого процесса для условий 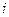- го опыта. Заполнение этого столбца производят, как будет показано далее при анализе результатов эксперимента и сравнения их с результатами «мысленных опытов», полученных при решении уравнения предполагаемой имитационной математической модели исследуемой области процесса.

Таблица 3

Матрица планирования и результаты экспериментов

при исследовании резистивных пленок

Номер опыта

Порядок проведения опыта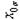

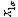
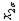
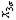
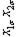
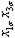
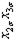
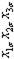
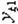
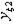
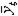
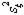
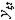
3 6 4 8 1 7 8 2 7 4 6 5 2 8 5 1

+ + + + + + + +

- + - + - + - +

- - + + - - + +

- - - - + + + +

+ - - + + - - +

+ - + - - + - +

+ + - - - - - +

- + + - + - - +

2,4 2,4 2,0 2,2 2,2 2,1 2,1 1,7

2,8 2,2 2,4 2,4 2,2 1,7 1,9 1,7

2,6 2,3 2,2 2,3 2,2 1,9 2,0 1,7

0,08 0,02 0,08 0,02 0,08 0,02

Примечание: для получения значения ТКС (функции отклика 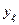) необходимо цифры, приведенные в 11, 12 и 13 столбцах табл. 14.1, умножить на —10⁴; единицей измерения ТКС является 1^оС.

Лекция 15

Дробный факторный эксперимент

При большом числе учитываемых в эксперименте факторов ПФЭ становится громоздким и занимает очень большое время для своего проведения, так как число опытов с ростом 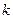увеличивается по экспоненте. Правда, при этом уменьшаются ошибки при определении коэффициентов полинома, так как для оценки каждого из них используются все опыты.

Однако число опытов можно сократить, если априори известно, что на процесс не оказывают влияния те или иные взаимодействия. Действительно, в реальной ситуации некоторые взаимодействия факторов особенно высокого порядка (т. е. включающих большое число символов) не влияют на выходной параметр. В этом случае можно использовать так называемые дробные реплики от ПФЭ или дробный факторный эксперимент (ДФЭ).

Предположим, что необходимо получить математическое описание процесса при трех учитываемых факторах и 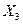, оказывающих влияние на функцию отклика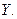

При использовании ПФЭ для определения коэффициентов полинома 1-го порядка необходимо провести восемь опытов (2³) в соответствии с матрицей планирования, приведенной в табл.13.2. Число номеров опытов должно быть не менее числа коэффициентов полинома, в соответствии с которым планируется эксперимент. В данном случае предполагаемая математическая модель, описывающая исследуемый процесс, имеет вид полинома (12.1), содержащего восемь коэффициентов от 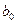до 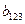. Однако, если взаимодействие между факторами и 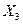отсутствует, можно ограничиться четырьмя опытами. В этом случае можно воспользоваться матрицей планирования ПФЭ для двух факторов 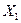и 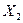, приведенной в табл.13.1, заменив в вей обозначение 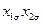на 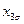соответствующее безразмерному значению фактора 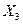на верхнем и нижнем его уровнях. Чередование знаков в этом столбце соответствует результату перемножения безразмерных значений двух других факторов ( ), т. е. остается неизменным после замены символов в матрице планирования, которая после введения в нее третьего фактора остается ортогональной. Эксперимент в этом случае будет ставиться уже с включением третьего фактора, изменяющегося согласно столбцу 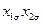ПФЭ (табл.13.1), а предполагаемая математическая модель будет иметь вид полинома 1-го порядка, не учитывающего взаимодействия факторов, т. е.

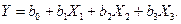(15.1)

Такой сокращенный план содержит половину опытов от требуемого их числа 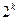согласно плану ПФЭ (в нашем случае четыре опыта вместо восьми) и называется полурепликой от ПФЭ типа 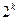. Условное обозначение такого плана: ДФЭ типа 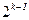, где 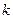- число учитываемых в эксперименте факторов; 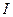- число взаимодействии, замененных факторами, учитываемых в эксперименте.

Для рассматриваемого случая трех факторов 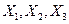матрица планирования ДФЭ типа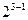 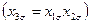будет иметь вид:

Номер опыта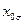
	+ + + +	- + - +	- - + +	+ - - +

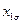
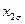
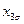
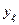
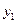
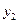
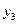
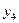
Приведенное планирование эксперимента дает возможность при обработке и анализе его результатов оценить в полиноме (15.1) свободный член 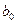и коэффициенты при линейных членах .

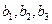Однако при этом предполагается, что коэффициенты 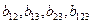в полиноме (13.2) равны нулю. Поэтому составление такой матрицы планирования эксперимента возможно лишь в том случае, если полностью отсутствует или пренебрежительно мало влияние на функцию отклика факторов взаимодействия факторов исследуемого процесса. Только в этом случае математическая модель, представленная полиномом, в котором отсутствуют члены, учитывающие эти взаимодействия (так как соответствующие им коэффициенты равны нулю), может быть адекватна исследуемому процессу.

При использовании матрицы планирования ДФЭ нужно всегда помнить, что мы получаем совместную оценку нескольких эффектов: факторов и их взаимодействий. Действительно,

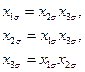(15.2)

Поэтому подсчитываемые в дальнейшем значения линейных коэффициентов 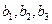полинома по экспериментальным значениям функции отклика будут всегда включать также значения коэффициентов, учитывающих эффект влияния взаимодействия факторов на функцию отклика (в нашем случае это коэффициенты 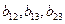). В результате этого подсчитанные значения коэффициентов полинома (15.1) фактически будут иметь следующий вид:

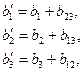(15.3)

где 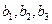- действительные значения линейных коэффициентов полинома (15.1); 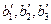- полученные их значения при наличии эффекта влияния взаимодействия факторов на функцию отклика.

Лекция 16

Обработка и анализ результатов эксперимента

Статистическая проверка гипотез о свойствах эксперимента

С целью повышения достоверности полученных в результате эксперимента значений функции отклика, проводят ряд параллельных опытов, число 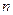которых определяет сам исследователь, исходя из конкретных условий проведения эксперимента, характера исследуемого объекта и выбранного плана эксперимента. Однако при проведении параллельных опытов исследователь должен быть уверен в воспроизводимости эксперимента т. е. в том, что все полученные в 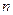опытах значения функции отклика 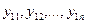являются результатом случайного рассеяния, а не результатом доминирующего действия какого-либо неконтролируемого и неуправляемого воздействия, которое может возникнуть при проведении опыта. Если при проведении эксперимента отсутствует такое доминирующее воздействие, то на основании центральной предельной теоремы [2] при возрастании числа параллельных опытов распределение экспериментальных значений функции отклика будет подчиняться закону Гаусса (нормальному закону).

Соответствие экспериментального распределения случайной величины предполагаемому теоретическому закону распределения можно оценить с помощью критерия Пирсона.

Критерий Пирсона и его применение в общем виде для оценки соответствия экспериментального распределения предполагаемому теоретическому можно проиллюстрировать на следующем примере.

Предположим, что имеется статистический ряд наблюдений над случайной величиной 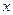. Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина имеет предполагаемый теоретический закон распределения.

Первоначально статистический ряд разбивают на 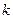интервалов и подсчитывают число значений случайной величины 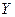в каждом интервале. В результате получают экспериментальный ряд частот

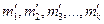
Следует сразу отметить, что предпосылкой применения критерия 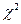является достаточная заполненность интервалов. На практике рекомендуется иметь в каждом интервале не менее 5 ÷10 наблюдений. Если число наблюдений в отдельных интервалах мало, имеет смысл объединить эти интервалы.

Исходя из предполагаемого теоретического закона распределения вычисляют частоты 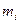в тех самых интервалах, на которые разбит статистический ряд. В результате получают теоретический ряд частот в 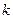интервалах: .

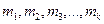Для проверки согласованности теоретического и экспериментального распределений подсчитывают меру распределения

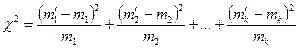или 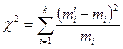(16.1)

и число степеней свободы 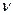. Число степеней свободы в этом случае равно числу интервалов 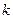минус число ограничений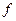

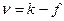(16.2)

Число ограничений равно числу параметров в рассматриваемом законе распределения, увеличенному на единицу. Например, для гауссовского закона имеются два параметра [M(x) и σ]; в этом случае число ограничений равно трем, а экспоненциальный закон характеризуется одним параметром λ, т. е. число ограничений для него равно двум.

Для распределения 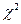составлены специальные таблицы. Пользуясь этими таблицами, можно для каждого значения 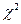и числа степеней свободы 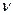, являющихся входами определить вероятность Р того, что за счет чисто случайных причин мера расхождения теоретическою и экспериментального распределения (16.1) будет меньше чем фактически наблюдаемое в данной серии опытов значение 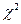. Если эта вероятность Р мала (настолько, что событие с такой вероятностью можно считать практически невозможным), то результат опыта следует считать противоречащим гипотезе о том, что закон распределения величины 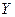является гауссововским. Эту гипотезу следует отбросить как неправдоподобную.

Напротив, если вероятность 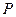сравнительно невелика, можно признать расхождение между теоретическим и экспериментальным распределениями несущественным и отнести его за счет случайных причин. Гипотезу о том, что величина 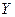распределена по нормальному закону, можно считать в этом случае правдоподобной, по крайней мере не противоречащей экспериментальным данным.

Критерий Кохрена. Этот критерий применяется для оценки однородности дисперсии только при равном числе повторов каждого эксперимента.

Для применения критерия Кохрена рассчитывается дисперсия экспериментальных значений функции отклика в каждой строке матрицы планирования эксперимента (14.2). В результате получается ряд значений выборочных дисперсий 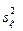(см. столбец 14 табл. 14.1). Очевидно, что недоверие будут вызывать именно наибольшие их значения. В эксперименте, проведенном в соответствии с ПФЭ типа 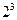в примере 4, таким значением будет 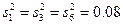, полученное в экспериментах соответственно 1-го, 3-го и 6-го номеров опытов.

Далее подсчитывается параметр

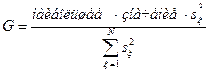, (16.3)

при 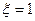, …, , т. е. вычисляют отношение максимального значения изменчивости среди 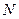опытов к сумме изменчивостей во всех 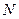опытах.

Найденное по (16.3) наибольшее экспериментальное значение 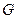сравнивают с критичным его значением .

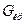Критичное значение 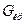представляет собою максимально возможное значение параметра 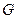при котором гипотеза о воспроизводимости эксперимента еще может считаться справедливой. В этом случае максимальная изменчивость функции отклика, полученная в результате проведения 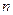параллельных опытов, не отличается от ожидаемой среди 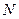опытов. Поэтому, если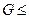 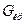то «подозрительное» максимальное значение изменчивости не является «инородным», а представляет собой результат случайного рассеяния исследуемой функции отклика, т. е. эксперимент воспроизводим. В противном случае, когда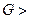 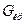- эксперимент не воспроизводим, и необходимо повторить его в анализируемой экспериментальной точке, добившись воспроизводимости,

т. е. выполнения .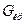

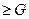Критичное значение отношения рассматриваемой изменчивости к сумме всех изменчивостей находят из таблицы критических значений критерия Кохрена для гауссовского закона распределения значений функции отклика в генеральной их совокупности (см. табл. 4 приложения).

Задаваясь определенным значением коэффициента риска 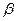(обычно задаются 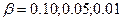), 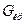определяют в столбце, соответствующем числу параллельных опытов 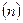и строке, соответствующей числу номеров опытов ( ).

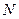Критерий Бартлета (В - критерий). Иногда бывает необходимо проверить гипотезу об однородности дисперсий при различных объемах выборки 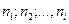. В этом случае пользуются критерием Бартлета. Для его вычисления определяют - среднюю арифметическую дисперсий