ГИ сфокусированного изображения 2 страница
Магнитный порошковый метод применяют для обнаружения трещин и
других дефектов на поверхности или вблизи ее в деталях из ферромагнитных
материалов любой формы независимо от вида термообработки. Метод основан на выявлении искажения магнитного поля около трещины или подповерхностного дефекта с помощью мелкодисперсных ферромагнитных частиц, выполняющих роль индикаторов. Эти частицы под действием магнитных сил перемещаются в места наибольшей концентрации силовых линий — к зонам дефекта и образуют контрастные накопления в виде линий или пятен. Намагничивание деталей проводят при определенном направлении магнитного потока, создаваемого полюсными электромагнитами, или пропусканием электрического тока через деталь. Направление силовых линий в детали выбирают перпендикулярным ожидаемому направлению трещин. Порошок или суспензию в зависимости от магнитных свойств материалов наносят в присутствии намагничивающего поля (магнитомягкие материалы) или в условиях остаточной намагниченности (магнитотвердые материалы). Магнитный контроль трещин широко применяют в машиностроении и двигателестроении для контроля стальных деталей после финишных технологических операций и термообработки.
Метод вихревых токов (электромагнитный метод) применяют для контроля электропроводящих материалов, заготовок и деталей на различных этапах производства и эксплуатации. Им обнаруживают поверхностные и подповерхностные трещины и дефекты» локальные коррозионные поражения (межкристаллитную коррозию), особенности структуры после термообработки. Измерением проводимости определяют зону, поврежденную огнем, или область коррозионных повреждений, а также осуществляют разбраковку материалов по маркам. С помощью вихретоковых дефектоскопов измеряют толщину листов, стенок, различных защитных покрытий, остаточных толщин после химического фрезерования и коррозии. Новые разработки по вихретоковому методу привели к созданию приборов для контроля многослойных неразъемных конструкций. Метод основан на индукционном возбуждении вихревых токов в электропроводящем материале объекта и регистрации изменений электромагнитного поля этих токов в связи с трещиной или дефектом в поверхностном слое детали. Источником и приемником электромагнитных колебаний является одна или несколько катушек индуктивности.
Радиационные методы обнаружения трещин и дефектов, а также нарушений внутренней конфигурации и взаимного расположения деталей, не доступных для осмотра при изготовлении, сборке, ремонте и эксплуатации, применяются для контроля слитков и отливок, сварных соединений, паяных и клепаных соединений, железобетонных изделий, неразъемных деталей самолетов, агрегатов и узлов конструкций.
ГОСТ 20426—82 на радиационные методы классифицирует их по принципу регистрации и наблюдения дефектов, а не по принципу жесткости излучения: радиографический (рентгеновское, гамма- и бета-излучение); электрорадиографический (рентгеновский); радиоскопический (рентгеновский, бетатронный); радиометрический (применение рентгеновских аппаратов, радиоактивных источников, бетатронов).
Радиационные методы выявляют подповерхностные и внутренние трещины и дефекты в деталях из любых материалов на основе ослабления или усиления ионизирующего изучения, вызванного дефектом и зафиксированного преобразователями излучений: радиографической пленкой, фотобумагой, электрорадиографической пластиной, флуороскопическим экраном, сцинтилляционным монокристаллом с электронно-оптическим преобразователем, рентгенотелевизионной установкой с рентгеновидиконом, с помощью ксерографии.
Акустические ульразвуковые (УЗ) методы и их разновидности эффективно применяют для обнаружения, измерения и определения координат трещин и дефектов. На их основе созданы и серийно выпускаются УЗ - дефектоскопы, интроскопы, полуавтоматические системы массового контроля. В УЗ - дефектоскопах используют методы, различающиеся по принципу действия и устройству приборов, а также по характеру измеряемых величин и мест расположения искателей (пьезодатчиков).
Теневой метод (метод сквозного прозвучивания, метод звуковой тени впервые был предложен в 1928 г. С.Я. Соколовым). Излучатель и приемник размещают по разным сторонам изделия. Трещина или другой дефект, находясь на пути ульразвуковой волны, ослабляет ее энергию (поглощает или рассеивает), что регистрируется приемником и определяется индикатором.
Импульсный эхо-метод. Излучатель генерирует короткий ультразвуковой импульс, который отражается от дефекта, поверхности и "дна" изделия. Часть лучей возвращается на искатель, который теперь работает в режиме приемника. Поскольку "донные" отраженные сигналы поступают на искатель позднее, чем сигналы от дефектов, их различают на индикаторе. По амплитуде эхо-сигналов судят о величине трещины (дефекта), а по времени от момента излучения импульса до момента приема эхо-сигнала определяют расстояние до обнаруженной трещины. Этот метод широко применяют практически для любых материалов и конструкций, выявляя трещины и другие несплошности в сварных соединениях, трубах, сосудах, паяных и клееных соединениях, при контроле сотовых конструкций и композиционных материалов. Конструкция искателей определяется формой изделия, направлением прозвучивания и способом контакта с поверхностью. Обычно для надежного контакта с целью обеспечения приема - передачи ультразвука без значительных потерь в контактную щель, соизмеримую с длиной УЗ-волны, вводят иммерсию - минеральные масла, глицерин или воду. В некоторых случаях зазор увеличивают для обеспечения иммерсии при непрерывном истечении струи под движущийся искатель. Некоторые схемы прозвучивания и виды искателей показаны на рис.10.1 и 10.2.
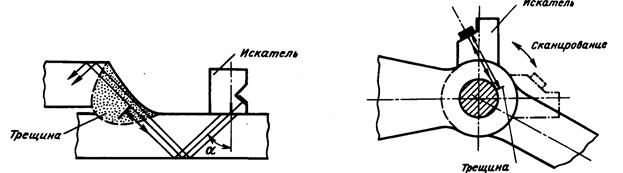
Рис. 10.1. Схема УЗ-контроля сварного Рис. 10.2. Схема УЗ-контроля проушины
соединения внахлестку с тещиной шарнирного узла со специальными
в шве насадками для искателя и наклонной
осью луча
Метод акустической эмиссии (АЭ). Процесс микротрещино-образования в деталях машин непосредственно связан с технологией производства материала и деталей, с режимами и условиями эксплуатации изделий. Излучение волн напряжений, обусловленное возникновением и развитием микродефектов (микротрещин) в материале, независимо от причины их появления (усталость, текучесть, термообработка, НДС, старение, вибровоздействие и т.д.) может быть обнаружено и зарегистрировано с высокой точностью современной акустической аппаратурой. Поэтому еще в начале 50-х годов началось интенсивное изучение "деформационных шумов". Физические причины возникновения упругих волн в структуре твердых тел связаны с поликристаллическим строением металлов и сплавов, их фазовым составом, а в неметаллических материалах — неидеальными связями между элементами многомерных структур и внутренним трением.
Экспериментально исследованы некоторые источники АЭ в твердых телах. Показано, что упругие волны напряжений возникают при движении скопления дислокации, двойниковании в кристаллах, фазовых превращениях в металлах и сплавах, образовании усталостных микротрещин, сопровождающемся эффектом динамической разгрузки материала в вершине трещины, пульсациями скоростей трещины и ее ветвления. Одновременно возникающие пластические деформации в вершине связаны со скольжением и двойникованием в кристаллах; кроме того трение поверхностей без смазочного материала, когда "слипание" по вершинам микронеровностей приводит к местным пластическим деформациям также регистрируется как сигналы АЭ.
Начало трещинообразования связано с сигналами АЭ различной интенсивности и амплитуды, поэтому для решения задачи обнаружения момента зарождения микротрещины проводится селекция сигналов АЭ по амплитудным, временным и спектральным параметрам. Во всех случаях нужны калибровка датчиков и аппаратуры и определение пороговых значений сигналов, на которые настраиваются приборы оповещения.
Определение местоположения вершины трещины по сигналам АЭ осуществляют на основе четырех пространственно разнесенных на объекте датчиков — пьезопреобразователей, осуществляющих локацию по измерению времени задержки между моментами поступления сигнала в соответствующие каналы приема и регистрации.
При циклическом нагружении конструкций толкование сигналов АЭ значительно усложняется вследствие шумовых помех, вызванных самой испытательной техникой, и физических особенностей. "Эффект Кайзера", заключающийся в невоспроизводимости сигналов АЭ при повторном нагружении до уровня напряжений первого нагружения, значительно снижается уровень синалов АЭ, которые становятся близки по амплитудам к внешним помехам.
Несмотря на недостатки метода АЭ, заключающиеся в сложности аппаратуры и анализа результатов, в привлечении к работам высококвалифицированного персонала, в необходимости подавления активных помех, требующих ряда дополнительных мероприятий, метод АЭ обладает рядом уникальных свойств: высокой чувствительностью определения сигналов АЭ; возможностью следить только за активным развивающимся дефектом, представляющим опасность для конструкции; использованием неподвижных (без сканирования) датчиков, устанавливаемых на значительных расстояниях от трещины; универсальностью в применении к явлениям в твердых телах от причин возникновения в них упругих колебаний.
Лекция 11
Моделирование сложных процессов
Понятие о моделях сложных процессов
Сложный процесс, как и любая сложная система, представляет собой составной объект, части которого можно рассматривать как составляющие системы, объединенные в единое целое в соответствии с определенными принципами или связанные между собой заданными отношениями. Части сложной системы (подсистемы) можно расчленить (часто лишь условно) на более мелкие подсистемы.
Свойства сложной системы в целом определяются, как свойствами составляющих ее элементов, так и характером взаимодействия между ними. Сложные системы характеризуются тем, что:
- состояние системы описывается, как правило, большим числом динамических переменных;
- система обнаруживает качественные изменения динамического поведения;
- система включает нелинейные взаимодействия и обратные связи, которые так же, как правило, содержат нелинейности.
Конечной задачей современного эксперимента, как правило, является разработка модели, адекватной исследуемому процессу.
Под адекватностью понимают верное воспроизведение в модели связей и отношений исследуемого процесса. Степень адекватности определяется соответствием модельных и экспериментальных результатов. В то же время, экспериментальное исследования сложных процессов должно дополняться моделированием, когда эксперименты ставятся в соответствии с предполагаемой моделью исследуемого процесса. Моделирование с одной стороны, позволяет четко поставить задачу эксперимента, а с другой, способствует анализу его результатов.
Большинство современных процессов характеризуется наличием значительного числа разнообразных факторов, на них влияющих и играющих роль возмущения.
Представив процесс в виде «черного ящика» (рис. 11.1), все многообразие действующих на его входе параметров (оказывающих влияние на выходной параметр процесса) можно разбить на три основные группы.
В этом случае состояние объекта - «черного ящика» характеризуется n-мерным вектором Y, называемым выходом системы, или вектором отклика, а его составляющие 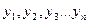 - параметрами, или функциями отклика.
- параметрами, или функциями отклика.

Рис. 11.1. Схема сложного процесса
Вектор отклика является функцией входных параметров, действующих в исследуемом процессе. Первая группа составляет 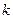 -мерный вектор
-мерный вектор 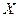 управляемых параметров, т. е. таких, которые можно измерять и целенаправленно изменять, поддерживая при этом некоторый заданный режим исследуемого процесса. Вектор
управляемых параметров, т. е. таких, которые можно измерять и целенаправленно изменять, поддерживая при этом некоторый заданный режим исследуемого процесса. Вектор 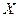 называют вектором факторов; его составляющие
называют вектором факторов; его составляющие 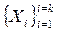 - факторы, а область их возможных значении в
- факторы, а область их возможных значении в 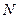 опытах
опытах 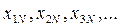 - факторным пространством.
- факторным пространством.
Вторая группа образует р - размерный вектор 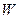 контролируемых, но неуправляемых параметров
контролируемых, но неуправляемых параметров 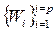 характеризующихся состоянием исходных функций отклика на операциях предшествующих исследуемому процессу (например, чистота исходною кремния, используемого в процессе изготовления микросхем). Они не поддаются целенаправленному изменению в исследуемом процессе.
характеризующихся состоянием исходных функций отклика на операциях предшествующих исследуемому процессу (например, чистота исходною кремния, используемого в процессе изготовления микросхем). Они не поддаются целенаправленному изменению в исследуемом процессе.
Третья группа входных параметров составляет m -мерный вектор 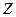 неконтролируемых, а следовательно и неуправляемых входных параметров
неконтролируемых, а следовательно и неуправляемых входных параметров 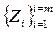 . Сюда относятся параметры, оказывающие случайные возмущающие воздействия на процесс.
. Сюда относятся параметры, оказывающие случайные возмущающие воздействия на процесс.
Очевидно, что выход системы 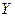 может состоять из любого числа функций отклика, интересующих исследователя обычно в разной степени.
может состоять из любого числа функций отклика, интересующих исследователя обычно в разной степени.
Вполне понято, что при исследовании процесса чаще всего работают именно с первой группой входных параметров. Однако следует помнить, что соответствие полученных результатов эксперимента исследуемому процессу зависит от того, настолько полно в модели будут учтены вес те входные параметры, которые в большей степени влияют на функцию отклика и ее конкретные значения 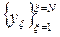 , фиксируемые в процессе проведения каждого
, фиксируемые в процессе проведения каждого
из 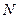 опытов.
опытов.
При моделировании, как правило, анализируется не все многообразие явлений, определяющих исследуемый процесс, а лишь те, которые существенны для решения поставленной задачи.
Модель — это упрощенная система, отражающая отдельные, наиболее важные стороны явлений изучаемого процесса. Один процесс можно описать различными моделями, в то время как одна модель может описывать различные процессы. При этом удается использовать результаты моделирования одних процессов для описания других, полученных с учетом их различной физической природы.
Процесс моделирования должен удовлетворять следующим требованиям:
- эксперимент на модели должен быть проще, оперативнее и экономичнее, чем на объекте;
- должно быть известно правило, по которому можно перенести результаты исследования модели на объект.
Классификация моделей
На практике различают два вида моделирования: физическое и математическое.
Физическое моделирование — воспроизведение постоянства определяющих критериев подобия.
Физической моделью некоторой системы называют систему той же или иной природы, которая частично или полностью воспроизводит свойства (главным образом—динамические) исходной системы (объекта моделирования) в рамках заданного приближения.
При физическом моделировании для исследования процесса в качестве физической модели часто используют процесс другой физической природы, описываемой аналогичным математическим аппаратом.
Математическое моделирование — это метод качественного и (или) количественного описания процесса с помощью так называемой математической модели, при построении которой реальный процесс или явление описывается с помощью того или иного адекватного математического аппарата.
Моделируемые процессы весьма разнообразны по своей природе и степени сложности. В связи с этим существуют различные подходы к их анализу и способу построения моделей.
Все процессы делятся на детерминированные и стохастические.
Детерминированными называются такие процессы, динамика которых полностью определяется начальными условиями, и динамические переменные являются функциями времени. По этому динамику можно однозначно предсказать на основе изучения его механизма. Стохастическими процессами называются такие, параметры которых изменяются случайно, под воздействием неконтролируемых дестабилизирующих воздействий, поэтому однозначно предсказать поведение таких процессов на основе их изучения затруднительно; можно говорить лишь о вероятности того или иного типа их поведения.
В соответствии с характером изучаемого процесса строятся жесткие или вероятностные модели.
Жесткие (детерминированные) модели строятся обычно без использования статистических вероятностных распределений. В этом случае определенному значению входного параметра процесса соответствует вполне определенное значение его выходного параметра. Связь между входным и выходным параметрами в этом случае является функциональной связью.
Значительно сложнее обстоит дело с вероятностными моделями, описывающими стохастические процессы. Большинство изучаемых современных процессов носят, как правило, случайный характер, когда выходной параметр связан с входным параметром статистически, т.е. нельзя заранее с точностью, характерной для функциональной связи, предсказать значение выходного параметра, соответствующее определенному значению входного. В случае статистической связи выходного параметра 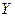 с входным
с входным 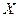 , каждому определенному значению
, каждому определенному значению 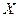 соответствует не определенное значение
соответствует не определенное значение 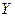 (как в случае функциональной связи), а распределение значений
(как в случае функциональной связи), а распределение значений 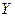 , изменяющегося с изменением
, изменяющегося с изменением 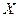 . Поэтому вероятностные модели (когда решение принимается в условиях неопределенности) строятся с использованием методов теории вероятностей и математической статистики.
. Поэтому вероятностные модели (когда решение принимается в условиях неопределенности) строятся с использованием методов теории вероятностей и математической статистики.
Для построения математической модели, отображающей зависимость функции отклика 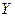 от фактора
от фактора 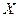 , статистические данные, обрабатывают, подсчитывая средние значения сначала, например, функции отклика
, статистические данные, обрабатывают, подсчитывая средние значения сначала, например, функции отклика 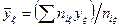 для каждого определенного значения
для каждого определенного значения 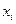 , которые наносят на прямоугольную систему координат, где по оси ординат откладывают значения
, которые наносят на прямоугольную систему координат, где по оси ординат откладывают значения 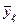 а по оси абсцисс - соответствующие им значения
а по оси абсцисс - соответствующие им значения 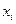 . Аналогичным образом находят средние значения
. Аналогичным образом находят средние значения 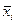 для каждого значения
для каждого значения 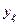 и также наносят на соответствующую прямоугольную систему координат. По виду графического изображения обработанных экспериментальных данных судят о наличии влияния одного параметра на другой. Если такое влияние обнаружено, то можно говорить о наличии, так называемой, корреляционной связи между рассматриваемыми параметрами. Полученные экспериментальные кривые называют кривыми регрессии, которые, в свою очередь, могут быть представлены уравнениями вида
и также наносят на соответствующую прямоугольную систему координат. По виду графического изображения обработанных экспериментальных данных судят о наличии влияния одного параметра на другой. Если такое влияние обнаружено, то можно говорить о наличии, так называемой, корреляционной связи между рассматриваемыми параметрами. Полученные экспериментальные кривые называют кривыми регрессии, которые, в свою очередь, могут быть представлены уравнениями вида 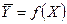 и
и 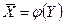 , называемыми уравнениями регрессии соответственно
, называемыми уравнениями регрессии соответственно 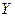 на
на 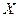 и
и 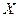 на
на 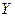 . Насколько тесна корреляционная связь и является зависимость между рассматриваемыми параметрами прямолинейной или криволинейной, — объективный ответ даст проведение корреляционного и регрессионного анализа результатов экспериментальных данных.
. Насколько тесна корреляционная связь и является зависимость между рассматриваемыми параметрами прямолинейной или криволинейной, — объективный ответ даст проведение корреляционного и регрессионного анализа результатов экспериментальных данных.
Целью корреляционного анализа является установление тесноты корреляционной связи между рассматриваемыми параметрами, а целью регрессионного анализа — установление формы этой связи (является ли корреляционная связь прямолинейной или криволинейной и каким конкретно уравнением регрессии она может быть описана). При этом могут возникнуть следующие варианты.
1. Оба признака 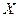 и
и 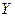 тесно связаны друг с другом.
тесно связаны друг с другом.
2. Оба признака 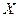 и
и 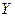 не строго связаны между собой, и их связь носит статистический характер.
не строго связаны между собой, и их связь носит статистический характер.
3. Оба признака 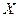 и
и 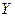 не связаны между собой. В этом случае значения признака
не связаны между собой. В этом случае значения признака 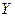 не меняются с изменением
не меняются с изменением 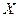 , и наоборот.
, и наоборот.
Физическое моделирование
Как известно, существует два подхода к изучению физики и соответственно к физическому моделированию процессов.
В первом из них, при изучении физики последовательно излагают физические явления, основу которых составляют различные физические процессы. В этом случае при физическом моделировании в качестве модели процесса берется модель той же физической природы, что и исходный процесс.
Возможен и иной подход, который имеет тенденцию к расширению. Речь идет о классификации физических явлений на основе их общих черт, проявляющихся, в первую очередь, в идентичности математического аппарата, который описывает эти явления. При этом оказывается, что один и тот же математический аппарат может описывать явления, физическая сущность которых различна.
Основным требованием к физической модели, независимо от того, реализует ли она те или иные физические механизмы моделируемого процесса, является условие ее подобия исходному процессу.
Подобие - это условие, при котором возможен количественный перенос результатов эксперимента с модели на оригинал.
Применение методов теории подобия при физическом моделировании позволяет установить параметры модели, а также определить соответствующие параметры моделируемого процесса на основе данных, полученных при измерениях на физической модели.
Подобие модели и оригинала дает нам правило переноса результатов эксперимента с модели на оригинал с помощью критериев подобия.
Условия подобия предоставляют определенную свободу в выборе параметров модели, но при этом критерий подобия сохраняется неизменным.
Математическое моделирование
Математическая модель – описание объекта или процесса, выполненное на математическом языке.
Классификация математических моделей на основе особенностей применяемого математического аппарата. В ней можно выделить следующие их разновидности.
Математические модели с сосредоточенными параметрами. Обычно с помощью таких моделей описывают динамику систем, состоящих из дискретных элементов. С математической стороны — это системы обыкновенных линейных или нелинейных дифференциальных уравнений.
Математические модели с распределенными параметрами. Моделями этого типа описываются процессы диффузии, теплопроводности, распространения волн различной природы и т.п.
Математические модели основанные на экстремальных принципах.
Общеизвестна основополагающая роль принципа наибольшего действия в физике. Например, все известные системы уравнений, описывающие физические процессы могут быть выведены из экстремальных принципов.
Математические модели в виде интегро-дифференциальных уравнений. Во многих процессах, в которыхучаствует большое число объектов, существенную роль играет суммарный результат многих взаимодействий. В этих случаях основу математической модели составляют обычно интегро-дифференциальные уравнения.
Методология математического моделирования
Концепция последовательного усложнения разрабатываемой модели
Одним из важнейших первичных этапов математического моделирования является концепция моделирования. Не следует стремиться с самого начала работы к созданию адекватной модели рассматриваемого процесса, хотя эта цель должна, разумеется, существовать. Попытка сразу, с первого подхода, достигнуть высокой адекватности имеет шансы на реализацию только при наличии большого опыта математического моделирования именно в рассматриваемой области.
При моделировании в новой области можно рекомендовать следующий подход к решению задачи. На первом этапе следует создать «грубую» модель. Речь идет об учете только небольшого числа самых существенных факторов. Работа с такой моделью составит базу для создания следующей, более адекватной модели, в которую целесообразно включить дополнительный фактор по сравнению с теми, которые вошли в первую, самую грубую модель. Получив вторую модель, следует проверить, даст ли правильный результат предельный подход к первой модели. Этот переход можно осуществить, если, например, устремить к нулю какой – либо параметр, значение которого связано с дополнительным фактором, введенным во вторую модель. В результате предельного перехода будет получено уравнение «грубого» приближения и его решение. Такая проверка с помощью предельного перехода может быть проведена, как при численном решении задачи, так и при аналитическом.
Метод последовательного усложнения модели введением дополнительных факторов или процессов может продолжаться до достижения необходимой адекватности модели.
Переход к безразмерным переменным. Важным методологическим приемом, облегчающим решение задач математического моделирования, является введение безразмерных переменных. Очень часто безразмерные переменные вводят так, чтобы они изменялись от 0 до 1. Для этого в качестве 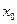 и
и 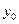 берут максимальные значения динамических переменных
берут максимальные значения динамических переменных 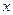 и
и 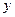 , которые обычно известны.
, которые обычно известны.
Анализ моделей
Расхождение между модельными результатами и данными наблюдений всегда существуют; можно считать, что эти расхождения являются мерой неадекватности модели.
Во многих случаях математическая модель дает только качественные описания реального объекта. Однако не следует думать, что это слабый результат. Знание особенностей поведения системы вносит значительный вклад в понимание исследуемого процесса.
Качественное описание объекта является первым этапом. Оно должно быть дополнено количественным описанием, т. е. моделированием с высоким уровнем адекватности.
Однако к высокому уровню адекватности не всегда целесообразно стремиться. Следует иметь в виду, что чем выше уровень адекватности, тем сложнее математическая модель, обеспечивающая этот уровень, и, следовательно, труднее ею пользоваться.
Оптимизация исследуемых процессов
Методы оптимизации
Одной из основных задач при исследовании различных процессов является возможность управления этим исследованием для обеспечения оптимальных условий его проведения. Наилучшим образом построить процесс, определить оптимальные режимы его проведения — естественные стремления исследователя. Однако до последнего времени эти вопросы очень часто решались интуитивно, на основе опыта разработчика и заказчика. Объясняется это необыкновенной сложностью современных процессов обилием и разнообразием всевозможных внутренних связей в них. Ведь для выбора оптимального процесса необходимо сравнить различные его варианты, учесть и проанализировать влияние огромного числа факторов на параметры продукта этого процесса. Вот почему столь велика роль интуиции, но оптимизация процесса в результате, как правило, не эффективна.
Одним из первых этапов при оптимизации технологических процессов является определение критерия оптимизации — функции отклика 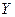 , значение которой будет положено в основу оценки процесса при его оптимизации. Задача оптимизации сводится к определению таких условий проведения технологического процесса, при которых критерий оптимизации достигает экстремума.
, значение которой будет положено в основу оценки процесса при его оптимизации. Задача оптимизации сводится к определению таких условий проведения технологического процесса, при которых критерий оптимизации достигает экстремума.
Дата добавления: 2015-08-08; просмотров: 844;
