Правила Кирхгофа. Эти правила используются для расчета разветвленных цепей.
Эти правила используются для расчета разветвленных цепей.
Для формулировки первого правила Кирхгофа введем понятие узла электрической цепи – это точка цепи, в которой сходятся три и более проводников. Тогда из закона сохранения электрического заряда следует
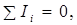
согласно которому алгебраическая сумма токов, сходящихся в узле, равна нулю.
Если записать закон Ома для замкнутой цепи, то из него следует второе правило Кирхгофа:
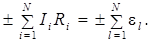
Согласно ему алгебраическая сумма падений напряжений на разных участках замкнутой цепи равна алгебраической сумме ЭДС, действующих в этой цепи.
 Для иллюстрации воспользуемся схемой, приведенной на рис. 8.6. Зададим произвольные направления токов на разных участках цепи и произвольные направления обхода в замкнутых контурах (например, указанные на рис. 8.6).
Для иллюстрации воспользуемся схемой, приведенной на рис. 8.6. Зададим произвольные направления токов на разных участках цепи и произвольные направления обхода в замкнутых контурах (например, указанные на рис. 8.6).
Записывая уравнения по первому правилу Кирхгофа, принято брать силу тока Iсо знаком «+», если ток входит в узел, и со знаком «-», если ток выходит из узла.
|
Используя правила Кирхгофа, запишем систему не зависимых уравнений (ни одно из них не является следствием других) для схемы рис. 8.6:
I1 – I2 + I3 = 0,
I1R1 + I2R2 = ε1,
I2R2 + I3R3 = ε2.
Если при решении этой системы уравнений окажется, что некоторые из токов имеют отрицательное значение, это означает, что эти токи имеют направление противоположное выбранным направлениям.
Лекция 9
9.1. Магнитное поле. Закон Био – Савара – Лапласа
В опыте Эрстеда проволока, по которой пропускался ток, была натянута над магнитной стрелкой, вращающейся на игле. При включении тока стрелка устанавливалась перпендикулярно к проволоке. Изменение направления тока заставляло стрелку повернуться в противоположную сторону. Из опыта следовало, что электрический ток создает в окружающем пространстве магнитное поле, которое должно характеризоваться векторной величиной. Эту величину назвали магнитной индукцией  .
.
 Опыты показывают, что для магнитного поля, как и для электростатического, справедлив принцип суперпозиции: поле
Опыты показывают, что для магнитного поля, как и для электростатического, справедлив принцип суперпозиции: поле  , порожденное несколькими токами, равно векторной сумме полей
, порожденное несколькими токами, равно векторной сумме полей 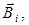 порожденных каждым током в отдельности:
порожденных каждым током в отдельности:
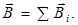
Лаплас обобщил результаты экспериментов Био и Савара в виде следующего дифференциального закона, названного законом Био – Савара – Лапласа
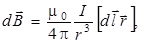 (9.1)
(9.1)
|
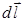 – вектор, численно равный длине
– вектор, численно равный длине 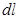 элемента проводника и совпадающий по направлению с током,
элемента проводника и совпадающий по направлению с током, 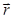 – радиус-вектор, проведенный из элемента проводника
– радиус-вектор, проведенный из элемента проводника 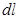 в рассматриваемую точку поля,
в рассматриваемую точку поля, 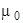 – магнитная постоянная (рис. 9.1).
– магнитная постоянная (рис. 9.1).
Закон Био – Савара – Лапласа позволяет определить магнитную индукцию поля, созданную проводниками различной формы, в интересующей нас точке пространства.
Применим формулу (9.1) для вычисления поля прямого тока (рис. 9.2а). Все векторы 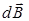 в интересующей нас точке имеют одинаковое направление (в нашем случае за чертеж). Поэтому сложение векторов можно заменить сложением их модулей. Модуль
в интересующей нас точке имеют одинаковое направление (в нашем случае за чертеж). Поэтому сложение векторов можно заменить сложением их модулей. Модуль 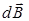 определяется выражением
определяется выражением
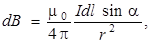 (9.2)
(9.2)
где α – угол между векторами 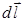 и
и 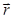 .
.


|
Из рис. 9.2а видно, что
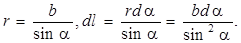
Подставим эти значения в формулу (9.2):
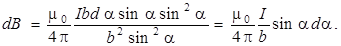
Угол α для всех элементов бесконечно прямого тока изменяется в пределах от 0 до π. Следовательно,
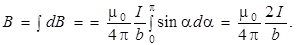
Таким образом, магнитная индукция поля прямого тока определяется формулой
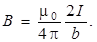 (9.3)
(9.3)
Линии магнитной индукции прямого тока представляют собой систему охватывающих провод концентрических окружностей (рис. 9.2б).
Дата добавления: 2015-08-08; просмотров: 919;
