Сила Лоренца. Закон Ампера
На заряд, движущийся в магнитном поле, действует сила, которую мы будем называть магнитной. Эта сила определяется зарядом q, скоростью его движения и магнитной индукцией 
в той точке, где находится заряд в рассматриваемый момент времени. Опытным путем установлено, что сила 
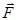, действующая на заряд, движущейся в магнитном поле, определяется формулой
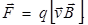(9.4)
Модуль магнитной силы равен
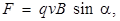
где α – угол между векторам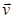и 
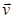и .
|
и . Если заряд qположителен, направление силы совпадает с направлением вектора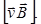 
В случае отрицательного qнаправления 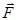и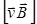 
противоположны (рис. 9.3).
Если имеются одновременно электрическое и магнитное поля, сила, действующая на заряженную частицу, равна
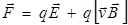. (9.5)
Это выражение было получено из опытов Лоренца и носит название силы Лоренца.
Если провод, по которому течет ток, находится в магнитном поле, на каждый из носителей тока, а, следовательно, на проводник действует магнитная сила. Опытным путем установлено, что на элемент проводника длиной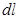 
с током в магнитном поле действует сила
|
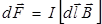, (9.10)
получившая название силы Ампера. Модуль этой силы вычисляется по формуле
,
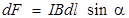где α – угол между векторами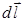 
и (рис. 9.4).
9.3. Теорема о циркуляции вектора магнитной индукции и теорема Гаусса для вектора
Можно доказать теорему о циркуляции вектора для вакуума: циркуляция вектора по произвольному замкнутому контуру Г равна алгебраической сумме токов, охватываемых этим контуром, умноженной на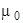 
:
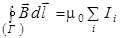. (9.11)
Знак силы тока в формуле (9.11) выбирается следующим образом: если направление тока связано с направлением обхода контура правилом правого буравчика, то это «+», если нет – «-».
В присутствии вещества в правую часть теоремы о циркуляции вектора необходимо ввести микротоки Iмикро, охватываемые контуром Г:
, (9.12)
где μ – относительная магнитная проницаемость среды.
Под микротоками, или молекулярными токами, понимают токи, вызванные движением электронов в молекулах. Эти токи создают магнитное поле вещества, помещенного во внешнем магнитном поле.
Из формулы (9.12) следует физический смысл теоремы о циркуляции вектора , а именно источником магнитного поля являются токи проводимости и микротоки. В природе не существует магнитных зарядов, поэтому линии являются замкнутыми.
Магнитное поле в отличие от электростатического – непотенциальное поле: циркуляция вектора магнитной индукции вдоль замкнутого контура, вообще говоря, не равна нулю и зависит от выбора контура. Такое поле называют вихревым или соленоидальным.
Так как в природе нет магнитных зарядов, линии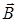 
являются замкнутыми, теорему Гаусса для вектора магнитной индукции запишем следующим образом:
.
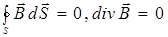Дата добавления: 2015-08-08; просмотров: 746;