Электроемкость конденсатора

Рассмотрим уединенный проводник, в окружающем пространстве которого нет других тел. Из формул электростатики следует, что заряд проводника qи его потенциал φ (он в условиях равновесия одинаковый внутри и на поверхности проводника) будут пропорциональны друг другу (q= c∙φ). Поэтому коэффициент пропорциональности между ними

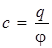(8.2)

не будет зависеть ни от qни от φ, он называется электроемкостью проводника. Электроемкость проводника характеризует его способность накапливать заряды и зависит только от геометрических размеров проводника, его формы и диэлектрических свойств окружающей среды (ε). Действительно, в случае металлической сферы можно записать:

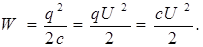(8.3)

Электроемкость уединенного проводника является достаточно малой величиной. Так, если рассматривать планету Земля как проводящий шар, то тогда ее электроемкость составит всего 711 мкФ. Эксперименты показывают, что приближение к проводнику каких-либо тел ведет к увеличению электроемкости этого проводника.

Наибольший эффект увеличения электроемкости проводника достигается для конденсаторов, представляющих собой две металлические пластины, разделенные слоем диэлектрика. На пластины (обкладки) подают заряды, одинаковые по модулю и противоположные по знаку. Форма обкладок конденсатора обеспечивает существование электрического поля только в пространстве между ними. Это позволяет устранить влияние на электроемкость конденсатора других тел.

На рис. 8.3 приведено схематическое изображение плоского, цилиндрического и

Электроемкость конденсатора вводится по формуле

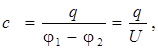(8.4)

где q– заряд положительно заряженной пластины конденсатора, φ₁ – φ₂ – разность потенциалов между его обкладками.

Запишем формулы для электроемкости конденсаторов разного вида.

1. Плоский конденсатор.

(8.5)

2. Цилиндрический конденсатор.

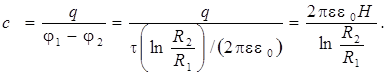(8.6)

3. Сферический конденсатор.

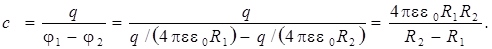(8.7)