Определение процесса

Термодинамический процесс, протекающий при неизменной теплоёмкости, называется п о л и т р о п н ы м.

Название “политропный” происходит от греческих слов “поли” – много и “тропос” – направление, путь. В политропном процессе в общем случае могут изменяться все термодинамические и калорические параметры кроме теплоёмкости, которую обозначают через c_п.

Вывод уравнения процесса.

Для вывода уравнения используем выражение первого закона термодинамики, записанное через энтальпию и внутреннюю энергию:

dq = di - vdp и dq = du + pdv.

Выразив через теплоемкости записанные выражения, получим:

c_п dT = c_p dT – vdp и c_пdT = c_v dT + pdv.

Отсюда

(с_п – с_p)dT = -vdp и (c_п –c_v)dT = pdv.

Разделим почленно первое уравнение на второе:

.

Здесь левая часть равенства определяется только теплоемкостью рабочего

Разделим почленно первое уравнение на второе:

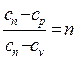. (2.43)

Проведя разделение переменных, получим:

n .

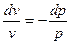После интегрирования этого соотношения в пределах от начала до конца процесса и антилогарифмирования, будем иметь:

p₁ v₁ⁿ = p₂ v₂ⁿ.

Отсюда следует, что

р vⁿ = const. (2.44)

Выражение (2.44) называется у р а в н е н и е м п о л и т р о п н ог о п р о ц е с с а. Оно устанавливает связь между параметрами состояния в процессе с теплоемкостью

c_n = const. Показатель степени n в уравнении называют п о к а з а т е - л е м п о л и р о п ы. Он принимает для каждого с_n конкретное числовое значение и, как изображено на рис.2.5, может меняться от - ∞ до +∞. Здесь зависимость теплоемкости политропного процесса от показателя n получена из (2.43) в виде

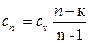. (2.45)

Рис. 2.5