Теплоемкость гав и газовых смесей
2.2.1. Понятие теплоемкости
Экспериментально установлено, что величина теплоты, необходимая
для изменения температуры конкретного количества вещества системы, пропорциональна разности конечной и начальной температур:
Q = C (T2 – T1),
где С – коэффициент пропорциональности.
В общем случае коэффициент С характеризует физическое свойство
системы, которое называется т е п л о е м к о с т ь ю.
Количественно теплоемкость равна теплоте, которой обменивается с окружающей средой система при изменении ее температуры на один кельвин. Аналитически это определение записывается в виде
С = 
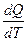 . (2.24)
. (2.24)
За единицу теплоемкости принят джоуль на кельвин (Дж/К). 
Теплоемкость, отнесенную к какой-либо количественной единице вещества, называют у д е л ь н о й. Для газов широко используются массовая, молярная и объемная удельные теплоемкости.
Массовая теплоемкость численно равна количеству теплоты, необходимому для изменения температуры одного килограмма газа на один кельвин.
Обозначают удельную массовую теплоемкость строчной буквой с и выражают в Дж/(кг· К).
Теплоемкость одного моля газа называют м о л я р н о й теплоемкостью. Ее обозначают 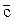 и выражают в Дж/(моль· К).
и выражают в Дж/(моль· К).
Теплоемкость единицы объема газа при нормальных физических условиях именуют о б ъ е м н о й теплоемкостью. Ее обозначают с′ и выражают  в Дж/(м3 ·К).
в Дж/(м3 ·К).
Массовая, молярная и объемная теплоемкости связаны соотношением:
с = 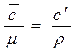 , (2.25)
, (2.25)
где 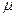 – молярная масса газа;
– молярная масса газа;
ρ – плотность газа при нормальных физических условиях.
Численное значение теплоемкости газа так же, как и теплоемкость твердых и жидких тел, зависит от его природы и уровня температуры, при которой она определяется.
Однако кардинальным отличием понятия теплоемкости газа от теплоемкости жидких и твердых тел является то, что на величину теплоемкости газа специфическое влияние оказывает характер процесса, в котором она вычисляется. Так, в адиабатном процессе, где dQ = 0, теплоемкость равна нулю. В процессе с постоянной температурой (T = const) теплоемкость равна бесконечности (c = ± ∞). Теплоемкость газа, присущую тому или иному процессу, принято обозначать индексом, характеризующим конкретный процесс. Если теплоемкость определяется в процессе при постоянном давлении, то ее обозначают cp и т.д.
2.2.2. Теплоемкости cp и cv
В термодинамике широко используются две теплоемкости – cp (в про-
цессе при постоянном давлении) и cv (в процессе при постоянном объеме). Проанализируем их особенности. С этой целью представим два цилиндра с поршнями (рис. 2.2). В цилиндрах находится по одному килограмму одного и того же газа. Первоначальные значения давления и удельного объема в цилиндрах одинаковы. Поршень в первом цилиндре закреплен, а во втором – может свободно перемещаться. Поставим задачу: изменить температуру газа в каждом цилиндре на одну и туже величину dT.
 . Рис. 2.2
. Рис. 2.2
Для цилиндра 1 запишем уравнение первого закона термодинамики в виде
dqv = du + pdv.
Разделим его на dT и, принимая во внимание, что dv = 0, получим:

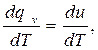
откуда
cv = 
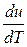 . (2.26)
. (2.26)
Интегрированием уравнения (2.26) от начального до конечного состояния процесса получим связь между изменением внутренней энергии и
температуры:
∆ u = cv ∆T. (2.27)
Проделав аналогичные операции с уравнением первого закона термодинамики для газа, находящегося во втором цилиндре, получим:
cp = 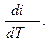 (2.28)
(2.28)
Отсюда следует соотношение между изменениями энтальпии и температуры в виде
∆i = cp ∆T. (2.29)
Теплоемкости в процессах при постоянном давлении и постоянном объеме имеют не только различные математические выражения, но и различные числовые значения. Так, доказывается, что cp >cv. Это видно из сравнения уравнений (2.26) и (2.28). Поскольку при одинаковом изменении температуры величина di > du, то, следовательно, cp > cv.
Обращаясь к рассмотренному примеру, можно пояснить сущность неравенства cp > cv. Так, при одинаковом изменении температуры газа в цилиндрах величина теплоемкостей определяется количеством подведенной теплоты. Ко второму цилиндру необходимо подвести больше теплоты, так как требуется не только изменить температуру газа на одно и то же число градусов, но и совершить некоторую работу расширения.
Можно определить, на сколько cp > cv. Для этого вычтем из (2.28) выражение (2.26) и, учитывая соотношение (1.6), получим:
cp – cv = 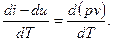
Дифференцируя уравнение состояния для 1 кг газа, будем иметь:
d(pv)=RdT
Следовательно,
cp – cv = R. (2.30)
Выражение (2.30) называется у р а в н е н и е м М а й е р а.Оно показывает, что для любого газа разность между теплоемкостями при p=const и v=const численно равна величине газовой постоянной этого газа.
Отношение теплоемкостей cp и cv называют п о к а з а т е л е м
а д и а б а т ы и обозначают буквой к, т.е.
 к =
к = 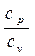 . (2.31)
. (2.31)
Величина к зависит от природы газа и всегда больше единицы. По известным значениям R и к можно вычислить как cp, так и cv, используя следующие выражения:
сp = 
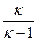 R , (2.32)
R , (2.32)
c v = 
 R . (2.33)
R . (2.33)
2.2.3. Зависимость теплоемкости от температуры
Теоретические исследования и опытные данные показывают, что при повышении температуры газа колебательные движения атомов в молекуле становятся интенсивнее. При этом для повышения температуры газа на каждый градус необходимо все большее количество энергии в форме теплоты. Таким образом, теплоемкость газа представляет собой функцию температуры. В общем случае зависимость теплоемкости газа от температуры можно представить в виде степенного ряда
c = c0 + α t + β t2 +  t3 +… , (2.34)
t3 +… , (2.34)
где c0 – значение теплоемкости при t = 0 0С;
α , β,  – числовые коэффициенты.
– числовые коэффициенты.
Значения c 0, α, β,  определяются эмпирическим путем.
определяются эмпирическим путем.
В качестве примера приведем квадратичную зависимость молярной теплоемкости азота от температуры:

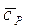 = 29,02 + 0,00531t + 0,000000127 t 2, кДж/(моль∙ К).
= 29,02 + 0,00531t + 0,000000127 t 2, кДж/(моль∙ К).
В диапазоне температур, имеющих место в современных тепловых машинах, зависимость теплоемкости от температуры с достаточной степнью
точности можно считать линейной. Это значит, что в уравнении (2.34)
можно учитывать только два первых слагаемых, т.е.:
c = c0 +α t (2.35)
Теплоемкость, соответствующую данной температуре, называют
и с т и н н о й. и вычисляют по уравнению (2.34) или (2.35).
В теплотехнических расчетах часто возникает необходимость знать с р е дн е е значение теплоемкости в определенном интервале температур.
Средней теплоемкостью cср данного процесса в интервале температур от t1 до t2 называют отношение теплоты процесса q1-2 к разности температур t2 – t1 , т.е.
cср = 
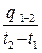 .
.
После подстановки значений q1-2 = 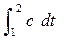 и с из (2.35), получим:
и с из (2.35), получим:
с с р =с0 + α 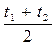 . (2.36)
. (2.36)
В Приложении табл.5 приведены значения истинной теплоемкости отдельных газов, а в табл. 6 – их средние значения в диапазоне температур от
0 до 2300 0С. При необходимости вычисления средней теплоемкости в диапазоне температур от t1до t2 можно применить формулу
сср 
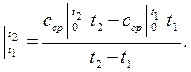 (2.37)
(2.37)
Показатель адиабаты к также зависит от температуры. Это можно показать, представив соотношение (2.31) в виде
к = 
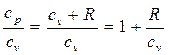 (2.38)
(2.38)
Экспериментальное изучение зависимости c = f (t) для идеальных газов показывает, что у каждого газа существует некоторый интервал температур, в котором его теплоемкость практически постоянна.
Идеальный газ в том интервале температур, где теплоемкость не изменяется, называется с о в е р ш е н н ы м..
Соотношения (2.27) и (2.29) справедливы только для совершенного оаза
Опытное изучение зависимости теплоемкости газов от давления показывает, что это влияние незначительное, и в практических расчетах его можно не учитывать.
2.2.4 Теплоемкость газовых смесей
В справочной литературе приводятся теплоемкости только для отдельных газов, в то время как при тепловых расчетах приходится встречаться с газовыми смесями. Ниже приведены выражения для вычисления теплоемкости смеси газов, если она задана парциальными давлениями, массовыми или объемными долями.
сp см = 
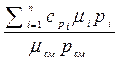 , cv cм =
, cv cм = 
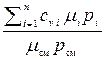 . (2.39)
. (2.39)
cp см = 
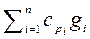 , cv cм =
, cv cм = 
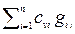 (2.40)
(2.40)
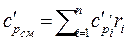 .
. 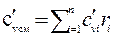 (2.41)
(2.41)
Для смеси газов справедливо уравнение Майера, которое будет иметь вид
сp см – сv см = R см. (2.42)
Дата добавления: 2015-08-04; просмотров: 1306;
