Термодинамические процессы

2.3.1. Понятие термодинамического процесса

Общее представление о состоянии системы и ее изменениях (процессах) изложено в подпункте 1.1.3.

Термодинамический процесс – это определенная последовательность изменения параметров состояния рабочего тела системы.

Термодинамические процессы могут быть равновесными и неравновесными, обратимыми и необратимыми. Если изменение состояния термодинамической системы протекает с нарушением ее внутреннего равновесия, то имеет место неравновесный термодинамический процесс. Реальные процессы, наблюдаемые в природе, в эксперименте, в машинах, являются неравновесными, их описание методами термодинамики невозможно.

С целью изучения основных свойств систем при обмене энергией с окружающей средой используют подход научной абстракции, идеализируют реальные процессы, принимая их за равновесные.

Термодинамический процесс, протекающий с бесконечно малым

отклонением состояния системы от равновесного, называется

р а в н о в е с н ы м.

Понятие об обратимых и необратимых процессах изложено в подпункте 1.1.5. Ниже рассматриваются только равновесные и обратимые термодинамические процессы идеального совершенного газа.

Для равновесной термодинамической системы связь между термодинамическими параметрами устанавливается уравнением состояния идеального газа (2.9). Следовательно, это уравнение справедливо и для равновесного термодинамического процесса не только в начальном и конечном состояниях системы, но и в любом промежуточном ее состоянии.

В общем случае в процессе могут изменяться произвольно (независимо) два термодинамических параметра из трех. Изучение работы тепловых машин показывает, что наибольший интерес для практики представляют конкретные термодинамические процессы, а именно изменения состояния, протекающие при постоянных давлении, объеме, и температуре, а также без теплообмена с окружающей средой. Их характерной особенностью является то, что для совершенного газа величина теплоемкости на всем протяжении процесса остается неизменной.

В термодинамике широко используются графические методы анализа процессов. При этом удобнее использовать не пространственные трехмерные изображения линий, описываемых функцией f(p,v,T), а их двухмерные проекции на одну из трех координатных плоскостей. Как правило, используется графическое изображение термодинамических процессов в координатах pv и Ts, а в особых случаях – в координатах i s; p i; id и др.

В pv и Ts – координатах на рис.2.3 и 2.4 показан произвольный

термодинамический процесс изменения параметров от состояния 1 до состояния 2.

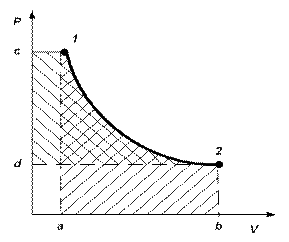
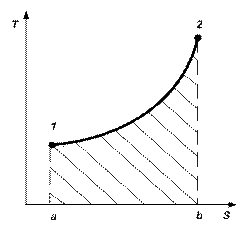
Рис 2.3 Рис. 2.4

На рис. 2.3 площадь, ограниченная кривой процесса 1-2, осью абсцисс и крайними ординатами a и b , как было показано в 1.2.5, численно равна работе расширения, а площадь, ограниченная кривой процесса, осью ординат и крайними абсциссами c и d, – технической работе.

В Ts - координатах площадь, ограниченная кривой процесса 1-2, осью абсцисс и крайними ординатами а и b, выражается интегралом:

F_{а-1-2- б} =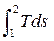

Поскольку dq = Tds или q = , то F_а-1-2-б численно равна подведенной теплоте в процессе.

Так как указанные площади зависят от характера процесса, то теплота и работа являются его функциями.

Независимо от особенностей процесс их анализа проводится в определенной последовательности, заключающейся в следующем:

– устанавливается характер процесса, назначается постоянный параметр;

– с использованием первого закона термодинамики и конкретных особенностей процесса выводится его уравнение;

– из уравнения процесса и уравнения состояния выводятся соотношения между термодинамическими параметрами;

– указывается способ построения графиков в координатах pv и Ts;

– определяется изменение внутренней энергии, энтальпии и энтропии рабочего тела;

– записываются выражения для работы расширения; работы технической и теплоты процесса;

– устанавливается количественное соотношение между теплотой, изменением внутренней энергии и работой в процессе.

Используя указанную последовательность, проведем анализ обобщенного для всех возможных процессов – п о л и т р о п н о г о.

2.3.2. Политропный процесс