При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы 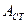 сторонних сил по перемещению заряда
сторонних сил по перемещению заряда  от отрицательного полюса источника тока к положительному полюсу, к величине этого заряда, называетсяэлектродвижущей силой источника (ЭДС):
от отрицательного полюса источника тока к положительному полюсу, к величине этого заряда, называетсяэлектродвижущей силой источника (ЭДС):
õ 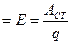 .(12.8)
.(12.8)
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении положительного единичного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
При перемещении положительного единичного заряда по замкнутой цепи постоянного тока работа сторонних сил равна ЭДС, действующей в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разбить на определенные участки. Участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными.
Немецкий физик Георг Ом (1787—1854) в 1826 году экспериментально установил, что ток 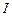 , текущий по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорционален напряжению
, текущий по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорционален напряжению  на концах проводника:
на концах проводника:
 , (12.9)
, (12.9)
где 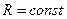 - электрическое сопротивление (или просто сопротивление) цепи.
- электрическое сопротивление (или просто сопротивление) цепи.
Это соотношение выражает закон Ома для однородного участка цепи: ток в проводнике прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению проводника.
В СИ единицей электрического сопротивления проводников служит 1 Ом. Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Проводники, у которых сопротивление является постоянной величиной, называются линейными. Графическая зависимость тока 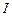 от напряжения
от напряжения  (такие графики называются вольтамперными характеристиками, или ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много устройств, не подчиняющихся линейному закону, например, полупроводниковый диод, биполярный и полевой транзисторы и др.
(такие графики называются вольтамперными характеристиками, или ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много устройств, не подчиняющихся линейному закону, например, полупроводниковый диод, биполярный и полевой транзисторы и др.
Закон Ома для неоднородного участка цепи, который содержит ЭДС 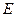 идеального источника энергии
идеального источника энергии
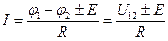 , (12.10)
, (12.10)
где 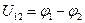 - напряжение между точками 1 и 2.
- напряжение между точками 1 и 2.
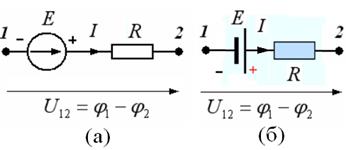
Знак плюс соответствует одинаковому направлению стрелки ЭДС (от минуса к плюсу) и тока (рис.12.1). Это соотношение называют обобщенным законом Ома.
|
| Рис. 12.1 |
Отметим, что идеальный источник ЭДС в теории цепей изображается в виде кружка со стрелкой (рис. 12.1 (а)), а в учебниках по физике – в виде батареи (рис. 12.1 (б)). В дальнейшем мы будем пользоваться первым обозначением.
Закон Ома для замкнутой цепи, которая содержит источник энергии с ЭДС 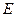
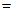 õ и внутренним сопротивлением
õ и внутренним сопротивлением  , и сопротивление нагрузки
, и сопротивление нагрузки 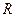 (рис. 12.2):
(рис. 12.2):
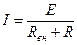 . (12.11)
. (12.11)

|
| Рис. 12.2 |
Эта формула выражает закон Ома для полной цепи: ток в полной цепи равен электродвижущей силе источника 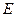 , деленной на сумму сопротивлений однородного
, деленной на сумму сопротивлений однородного 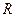 и неоднородного
и неоднородного  участков цепи.
участков цепи.
Если точки 1 и 2 закоротить (сопротивление закоротки равно нулю), то в цепи потечет ток короткого замыкания
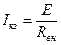 . (12.12)
. (12.12)
Ток короткого замыкания – максимальный ток, который можно получить от данного источника энергии с электродвижущей силой 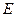 и внутренним сопротивлением
и внутренним сопротивлением  . У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызвать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызвать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
Если внешняя цепь разомкнута, то разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС:
 . (12.13)
. (12.13)
Величина, обратная сопротивлению проводника, называется электрической проводимостью:
 . (12.14)
. (12.14)
Единица проводимости 1 сименс (См): 1 См = 1 Ом-1. Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника с удельным электрическим сопротивлением  (удельной проводимостью
(удельной проводимостью 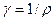 ), сопротивление
), сопротивление 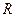 прямо пропорционально его длине
прямо пропорционально его длине 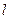 и обратно пропорционально площади его поперечного сечения
и обратно пропорционально площади его поперечного сечения  :
:
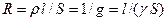 . (12.15)
. (12.15)
Закон Ома в форме (12.9) можно представить в дифференциальной форме.
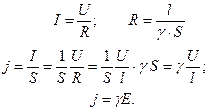
Для этого подставим сюда (12.14) и учтем (12.6):
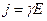 ,
,  . (12.16)
. (12.16)
Таким образом, плотность тока 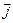 в любой точке внутри проводника прямо пропорциональна напряженности
в любой точке внутри проводника прямо пропорциональна напряженности  электрического поля в этой же точке. Это соотношение справедливо как для постоянных, так и для переменных полей.
электрического поля в этой же точке. Это соотношение справедливо как для постоянных, так и для переменных полей.
Отметим, что удельное электрическое сопротивление  и сопротивление
и сопротивление 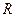 в первом приближении изменяются с ростом температуры по линейному закону:
в первом приближении изменяются с ростом температуры по линейному закону:
 ,
, 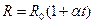 (12.17)
(12.17)
где  - удельное сопротивление при
- удельное сопротивление при  0°
0° 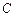 ,
, 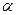 - температурный коэффициент,
- температурный коэффициент, 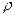 и
и 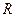 - величины при произвольной температуре
- величины при произвольной температуре 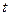 .
.
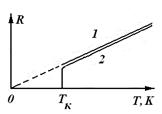
Температурная зависимость сопротивления проводника качественно представлена на рис. 12.3 (кривая 1). Впоследствии было обнаружено явление сверхпроводимости, которое заключается в том, что сопротивление многих металлов (например, алюминия, свинца, цинка и др.) и их сплавов при очень низких критических температурах 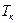 (0,14 — 20 К), характерных для каждого металла, скачкообразно уменьшается до нуля (кривая 2), т.е. металл становится абсолютным проводником.
(0,14 — 20 К), характерных для каждого металла, скачкообразно уменьшается до нуля (кривая 2), т.е. металл становится абсолютным проводником.
|
| Рис. 12.3 |
Впервые это явление было обнаружено в 1911 г. Г. Камерлинг-Оннесом для ртути. Явление сверхпроводимости объясняется на основе квантовой теории. Практическое использование сверхпроводящих материалов в настоящее время находится в стадии разработки. Сейчас обнаружены и активно исследуются материалы, обладающие сверхпроводимостью при температуре выше 100 К.
Дата добавления: 2015-08-04; просмотров: 1795;
