Конденсаторы. Конденсатор состоит из двух провод­ников (обкладок), заряженных зарядами q и − q, и разделенных диэлект­риком

Конденсатор состоит из двух провод­ников (обкладок), заряженных зарядами q и − q, и разделенных диэлект­риком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэ­тому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют плоские, цилиндрические и сферические конденсаторы.

Электроемкостью конденсатора называется отношение заряда q к напряжению U (разности потенциалов) между обкладками:

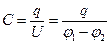. (11.15)

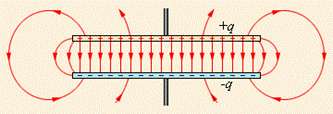
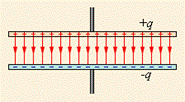
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора, в основном, локализовано между пластинами (рис. 11.7); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач можно приближенно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками (рис. 11.8). Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля.

Рис. 11.7

Рис. 11.8

Напряженность однородного поля, создаваемого двумя бесконечными параллельными разноименно заряженными плоскостями (поле внутри плоского конденсатора)

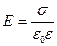. (11.16)

Тогда напряжение между обкладками конденсатора (10.23)

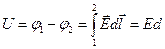, (11.17)

где 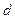- расстояние между пластинами.

Заряд пластин q =σS, (σ - поверхностная плотность заряда, S - площадь каждой пластины). Из этих соотношений получим формулу для электроемкости плоского конденсатора:

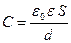. (11.18)

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в 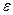раз.

Для расчета емкости цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусами 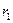, 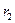( 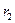> 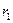), вставленных один в другой, пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Разность потенциалов между обкладками, заряженными с линейной плотностью 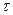, вычислим, используя формулу (10.32):

, (11.19)

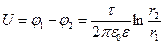. (11.20)

Учитывая, что заряд 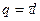, ( 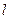- длина конденсатора), найдем емкость цилиндрического конденсатора

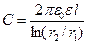. (11.21)

Для расчета емкости сферического конденсатора, состоящего из двух концентрических обкладок с радиусами 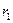, , 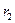разделенных сферическим слоем диэлектрика, используем формулу (10.31):

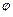
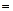
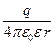
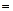
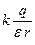. (10.31)

Разность потенциалов между обкладками конденсатора

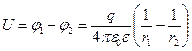. (11.22)

Отсюда емкость сферического конденсатора

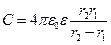. (11.23)

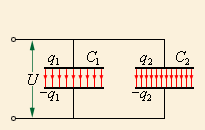
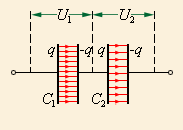
Конденсаторы могут быть соединены между собой параллельно (рис. 11.9) или последовательно (11.10).

Рис. 11.9

Рис. 11.10

При параллельном соединении конденсаторов напряжения на конденсаторах одинаковы U , а заряды равны, соответственно, q₁=C₁U и q₂=C₂₁U. Такую систему можно рассматривать как единый конденсатор с зарядом q= q₁+q₂ и напряжением U. Таким образом, емкость параллельно соединенных конденсаторов

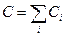. (11.24)

При последовательном соединении конденсаторов одинаковыми оказываются заряды обоих конденсаторов: q= q₁=q₂ =q, а напряжения на них равны, соответственно, U₁=q/C₁ и U₂=q/C₂. Такую систему также можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U=U₁+ U₂. Следовательно, при последовательном соединении конденсаторов складываются обратные величины емкостей:

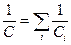. (11.25)