Характеристическое уравнение.

Свободный ток, то есть решение однородного дифференциального уравнения записывается в виде показательных функций Ае^pt ; то есть

i_св =Ае^pt

Для каждого тока ветви постоянная интегрирования – А (показатель затухания) одинаковы для свободных токов разных ветвей, что объясняется тем, что цепь охвачена единым переходным процессом.

Возьмем производную от свободного тока:

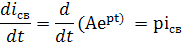
Возьмем вторую производную от :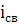

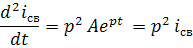
Найдем интеграл от :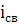

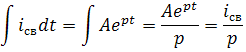
Подставляем значения 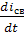, , 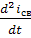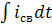в систему дифференциальных уравнений для свободных токов.

Для нашего примера получим:

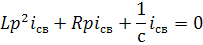
Сокращая 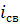получим характеристическое уравнение

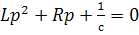или

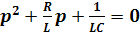
Составление характеристического уравнения системы дифференциальных уравнений является более сложной задачей. (Изучить самостоятельно!)

Составление характеристического уравнения методом входного сопротивления.

Характеристическое уравнение для определения р часто составляют более простым способом, составляют выражение входного сопротивления двухполюсника на переменном токе z(jω), заменяют jω на р получают z(р) и приравнивают его к 0.

z(р)=0

Это уравнение совпадает с характеристическим. Этот способ применим при отсутствии магнитной связи между ветвями.

В нашем примере

z(jω)=R+ jωL +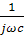

z(р)=R+pL +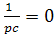

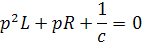
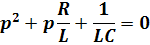
Этот способ особенно удобен в случае, когда переходный процесс описывается системой нескольких дифференциальных уравнений.

Как правило, не имеет значения в каком месте схемы определять входное сопротивление двухполюсника, так как вся цепь охвачена единым переходным процессом, однако, есть редкие исключения из правил, когда нужно определять z(р) со стороны той ветви, ток которой требуется определить на условии задачи.