Классический метод расчета переходного процесса.

Запишем уравнение по второму закону Кирхгофа для схемы, показанной на рисунке, при замкнутом ключе

U_L(t)+ U_c(t)+ U_R(t)=E

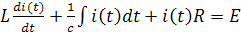
Продифференцируем все члены этого уравнения по t:

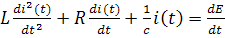
Это и есть дифференциальные уравнения (в нашем примере оно имеет второй порядок). Таким образом задача на переходный процесс сводится к решению дифференциального уравнения. Все три основных метода решения переходного процесса: классический, операторный и метод интеграла Дюамеля – основаны на решении дифференциального уравнения.

Классическим методом расчета переходных процессов называют метод, в котором решение дифференциального уравнения представляет собой сумму принужденной и свободной составляющих, а определение постоянных интегрирования, входящих в выражение для свободного тонка, производят путем совместного решения системы линейных алгебраических уравнений по известным значениям свободной составляющей тока и ее производных взятых при t=±0.

Расчет переходных процессов в линейных электрических цепях состоит из следующих основных операций:

1) Выбор положительных направлений токов в ветвях цепи;

2) Определение значений токов и напряжений непосредственно до коммутации;

3) Составление характеристического уравнения и определения его корней;

4) Получение выражения для искомых тонов и напряжений функции времени.

Для всех методов перечисленные операции являются обязательными, при этом первые три операции совершаются одинаково. Различие методов проявляется на четвертом, наиболее трудном этапе расчета.