Седиментационная устойчивость дисперсных систем

Седиментационная устойчивость - это способность дисперсной системы сохранять неизменным во времени распределение частиц по объему системы, т. е. способ­ность системы противостоять действию силы тяжести.

Чтобы оценить седиментационную устойчивость сис­темы, необходимо знать следующие характеристики: r — радиус частицы дисперсной фазы; ρ- плотность части­цы; ρ₀ — плотность дисперсионной среды; η— вязкость дисперсионной среды; V — объем частицы.

По закону Архимеда, на каждую частицу в системе действует сила тяжести (подъемная сила), равная:

F = mg = V ρg, (10.1)

где g — ускорение свободного падения. Эффективная масса частицы т' равна

m'=V( ρ- ρ ₀ ) . (10.2)

Если (ρ- ρ₀)>0, т. е. р > ро, частица будет оседать, если ρ<ρ₀ — частица будет всплывать. Примем, что ρ>ρ₀ Тогда частица дисперсной фазы будет оседать под действи­ем силы тяжести:

Fсед = m' g = V( ρ- ρ ₀ )• g. (10.З)

При оседании частицы в дисперсионной среде с вязко­стью г| возникает встречная сила — сила трения F_TP, про­порциональная скорости движения частицы:

F_TP = В • U_сед, (10.4)

где U_сед— скорость оседания частицы; В — коэффициент

трения.

Таким образом, чем больше скорость оседания, тем больше сила трения, замедляющая оседание. В результа­те устанавливается стационарный режим седиментации, которому соответствует F_сед = F_ТР, и частица оседает с по­стоянной скоростью.

Итак, V • (ρ- ρ₀) • g = В ■ U_сед, отсюда:

Uсед = V • (ρ- ρ₀) • g /B (10.5)

Часто для характеристики процесса седиментации ис­пользуют не скорость седиментации U_сед, а удельный по­ток седиментации I_сед.

Удельный поток седиментации — это число частиц, оседающих в единицу времени через сечение единичной площади, нормальное к направлению седиментации.

Размерность i_сед : [i_сед ]= част/см² • с.

Из определения i_сед следует:

Где ν— концентрация частиц в дисперсной системе.

Подставив в это уравнение значение U_сед из (10.5), получим

i_сед = V(ρ- ρ₀ ) •g• ν/B

Таким образом, удельный поток седиментации прямо пропорционален V, ν,( ρ- ρ₀ ) и обратно пропорционален В.

Для сферической частицы радиуса r V =4/3 π r³ , коэффици-

ент трения по уравнению Стокса В =6 π η r.Подставив эти

выражения в уравнение (10.6), получим:

i_сед =2 r²(ρ- ρ₀ ) •g• ν /B (10.7)

Значит, в случае сферических частиц удельный поток седиментации прямо пропорционален квадрату радиуса и обратно пропорционален вязкости среды.

Однако, рассматривая процесс седиментации, мы до сих пор не учитывали броуновского движения, в котором участвуют частицы микроскопических и коллоидных раз­меров. Следствием броуновского движения, как мы зна­ем, является диффузия, которая стремится выровнять концентрацию частиц по всему объему, в то время как седиментация приводит к увеличению концентрации в нижних слоях.

Таким образом, наблюдается два противоположных потока: поток седиментации i_сед и поток диффузии i_диф. Согласно уравнению (9.4),

i_диф = D (dν/dh), где D= kT /B

Каков же результат конкуренции этих потоков? Воз­можны три варианта:

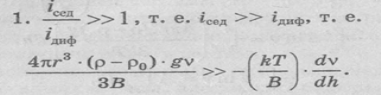
Чтобы выполнилось это неравенство, значения Т и dv /dh должны быть малы, а (ρ- ρ₀ ) и v — велики. В ре­альных условиях эти параметры заметно изменить слож­но, а радиус частиц в дисперсных системах изменяется в широком интервале: от 10^-7 до 10^{-2 см и именно радиус частиц является определяющим. Установлено, что дан­ное неравенство соблюдается, когда} r = > 10 ^-3 см. В этих случаях диффузией можно пренебречь, идет быстрая седиментация — система является седиментационно неустойчивой.

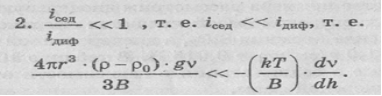
Это условие должно выполняться, когда Т и dv /dh велики, а а (ρ- ρ₀ ) и v — малы. Но и здесь решающую роль играет радиус частиц. Установлено, что это неравенство выполняется при r = < 10^{-5 см. В этом случае можно пренеб­речь седиментацией, диффузия приведет к равномерному распределению частиц по всему объему сосуда. Дисперс­ная система является седиментационно устойчивой.}

В системе имеет место седиментационно-диффузион-ное равновесие.

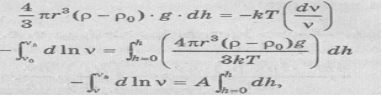
Проинтегрируем это уравнение, разделив переменные:

(10.8)

где νo — концентрация частиц на дне сосуда; ν_h, — кон­центрация частиц на высоте h от дна.

---гипсометрический закон Лапласа-Перрена.

В этом случае система является седиментационно-устойчивой, но распределение частиц в ней не равно­мерное, а равновесное. Это распределение наблюдается, когда 10^-5 < r < 10^{-3 см.}

В качестве примера рассмотрим дисперсную систему, в которой дисперсной фазой являются сферические час­тицы диоксида кремния SiO₂, а дисперсионной средой — вода, ρ₀ = 1,0 г/см³; η= 0,015 П. В таблице 10.1 приве­дены данные о седиментации в зависимости от радиуса частиц дисперсной фазы.

Из таблицы следует, что седиментация в лиофобных золях протекает очень медленно.

Итак, седиментационная устойчивость дисперсных систем определяется, главным образом, размерами час­тиц дисперсной фазы: • лиофобные золи (10^-7-10^-5см) — седиментационно ус­тойчивые системы, характерна диффузия, обеспечивающая равномерное распределение частиц по объему системы;

• микрогетерогенные системы (10^-5-10^{-3 см) — устанав­ливается седиментационно-диффузионное равновесие, для которого характерно гипсометрическое распреде­ление частиц по объему системы;}

• грубодисперсные (более 10^{-3 см) — седиментационно неустойчивые системы, происходит быстрая седимен­тация.}