Вычисление коэффициента корреляции между количеством осадков во II и III декадах июня (Х) и урожаем (У) яровой пшеницы
| Х, мм | У, ц/га | Отклонение от средней | Квадраты отклонений | Произведение | ||
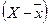
| 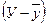
| 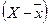 2 2
| 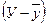 2 2
| 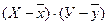
| ||
| 7,78 | -30 | -7,54 | 56,8516 | 226,20 | ||
| 16,50 | -22 | 1,18 | 1,3924 | -25,96 | ||
| 2,85 | -17 | -12,47 | 155,5009 | 211,99 | ||
| 2,76 | -12 | -12,56 | 157,7536 | 150.72 | ||
| 11,58 | -12 | -3,74 | 13,9876 | 44,88 | ||
| 17,44 | -12 | 2,12 | 4,4944 | -25,44 | ||
| 4,94 | -11 | -10,38 | 107,7444 | 144,18 | ||
| 18,44 | -7 | 3,12 | 9,7344 | -21.84 | ||
| 19,63 | 4,31 | 18,5761 | 68.96 | |||
| 16,30 | 0,98 | 0,9604 | 16,66 | |||
| 22,14 | 6,82 | 46,5124 | 163,68 | |||
| 29,69 | 14,37 | 206,4669 | 431,10 | |||
| 29,10 | 13,78 | 189,8884 | 427,18 | |||
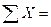 =502 =502
| 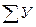 =199,15
=199,15
| 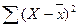 =5257 =5257
| 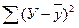 =969,8935
=969,8935
| ∑ 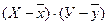 =1782,31
=1782,31
|
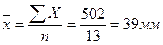 ;
; 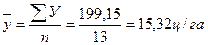
1. Коэффициент корреляции для выборочных наблюдений вычисляют по формул
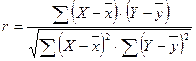
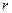 =
= 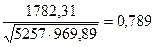 .
.
Не вычисляя отклонения и квадраты отклонений, корреляцию можно рассчитать по формуле
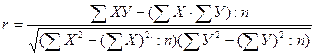 ,
,
где 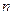 – число сопоставляемых пар (объём выборки).
– число сопоставляемых пар (объём выборки).
2. Степень связи между признаками более точно измеряется коэффициентом детерминации 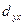 , равным квадрату коэффициента корреляции (
, равным квадрату коэффициента корреляции ( 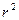 ) и показывающим долю тех изменений (%), которые зависят от изучаемого фактора. В нашем примере при
) и показывающим долю тех изменений (%), которые зависят от изучаемого фактора. В нашем примере при 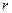 =0,8 не 80%, а только 64% изменчивости признака У обусловлена действием факториального признака Х (
=0,8 не 80%, а только 64% изменчивости признака У обусловлена действием факториального признака Х ( 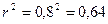 ), остальная часть корреляционной связи (
), остальная часть корреляционной связи ( 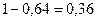 ) обусловлена другими факторами.
) обусловлена другими факторами.
3. Коэффициент корреляции выборочных наблюдений подвержен случайным колебаниям, которые зависят как от особенностей образования выборки, так и от точности наблюдений. Поэтому для оценки надёжности  определяют его ошибку
определяют его ошибку  и критерий существенности
и критерий существенности 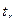 :
:
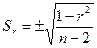 ;
; 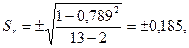
где 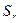 – ошибка коэффициента корреляции;
– ошибка коэффициента корреляции;
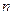 – число сопоставляемых пар (объём выборки).
– число сопоставляемых пар (объём выборки).
С увеличением объёма выборки 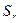 уменьшается, а точность определения
уменьшается, а точность определения 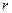 возрастает.
возрастает.
Критерий существенности коэффициента корреляции определяют по формуле
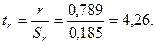
Если 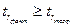 , то корреляционная связь существенна, а при
, то корреляционная связь существенна, а при 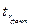 <
< 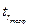 – несущественна.
– несущественна. 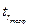 находят по табл. приложения 2 для 5%-ного, а при более строгом подходе – 1% - ного уровня значимости. Число степеней свободы принимают равным v
находят по табл. приложения 2 для 5%-ного, а при более строгом подходе – 1% - ного уровня значимости. Число степеней свободы принимают равным v 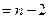 . В нашем примере при v=
. В нашем примере при v= 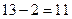 ,
, 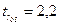 и
и 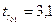 корреляционная связь существенна при 5%-ном и 1%-ном уровне значимости, так как
корреляционная связь существенна при 5%-ном и 1%-ном уровне значимости, так как 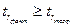 .
.
При достаточно большом числе наблюдений (не менее 100) коэффициент корреляции считается существенным, если он превышает свою ошибку в три и более раза, т.е. когда 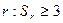 .
.
Дата добавления: 2015-08-04; просмотров: 1182;
