Разложение в конечную цепную дробь.

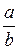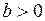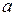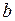Пусть рациональное число, причем . Применяя к и алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств.

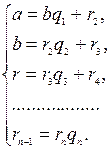
(1)

Системе равенств (1) соответствует равносильная система:

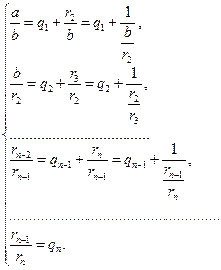
(2)

из которой последовательной заменой каждой из дробей 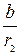, 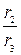и т. д. ее соответствующим выражением из следующей строки получается представление дроби 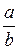в виде

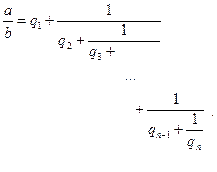
Такое выражение называется правильной конечной цепной дробью или правильной непрерывной дробью. При этом предполагается, что 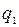– целое, а 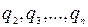– натуральные числа. Имеются различные формы записи цепных дробей:

1).

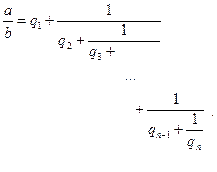
2).

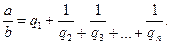
3). 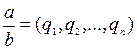и др.

Согласно последнему обозначению имеем

Числа 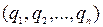– называются элементами цепной дроби.

Разложение рационального числа 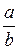имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на b является конечным.