Решение сравнений первой степени с помощью цепных дробей.

Рассмотрим сравнение

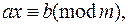(1)

где 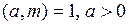(случай 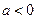сводится к данному).

Разложим 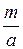в непрерывную дробь и обозначим ее подходящие дроби через 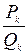, где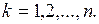

Тогда, согласно свойству несократимости подходящих дробей, получим 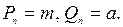Поэтому вместо соотношения

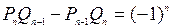
Имеем ,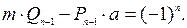

Отсюда

,

или (так как 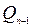– целое число)

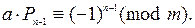
Умножая обе части этого сравнения на 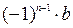, получим

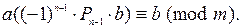
Сравнивая это сравнение с исходным (1), приходим к выводу, что оно имеет решение

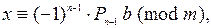
(2)

где 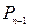– числитель предпоследней дроби в разл