Подходящие дроби и некоторые их свойства.

Рассмотрим дроби вида

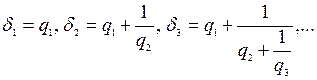
или

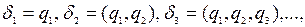
которые называются подходящими дробями данной непрерывной дроби или соответствующего ей числа . Заметим, что = = .

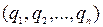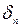Считается, что подходящая дробь 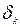имеет порядок 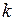. Заметим, что 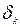переходит в 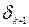, если в первой заменить 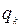выражением .

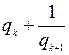Имеем,

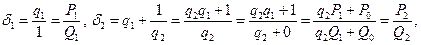
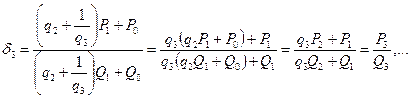
При этом принимается, что 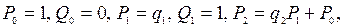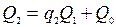и т. д. Закономерность, которую мы замечаем в построении формулы для 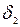(ее числителя 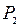и знаменателя 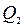) сохраняется при переходе к 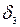и сохраняется также при переходе от 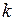к 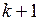, поэтому на основании принципа математической индукции для любого 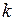, где 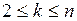, имеем

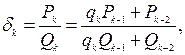
(1)

причем

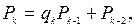и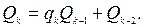

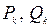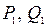Применяется следующая схема, в которую последовательно записываются значения , от до 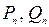по формулам (1).

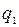
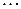
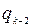
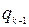
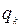
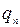
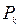
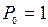
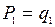
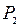
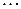
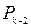
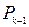
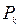
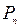
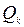
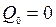
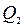
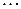
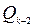
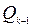
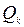
Отметим некоторые свойства подходящих дробей.

1). Пусть 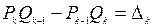. Так как по формулам (1)

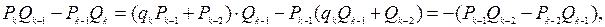то

.

Откуда видно, что все 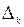имеют одинаковые абсолютные значения, а их знаки чередуются. Но

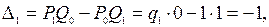
поэтому для любого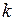

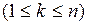
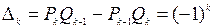
(2)

Формула (2) показывает, что .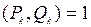

Так как если было бы 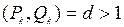, то получили бы противоречие, потому что из этого следовало бы, что 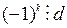, что невозможно. Значит все подходящие дроби 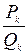являются несократимыми.

2). При помощи формулы (2) легко установить разность двух соседних подходящих дробей. Действительно, так как

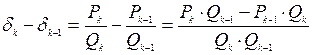, то

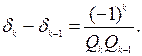
(3)

Отсюда расстояние между двумя соседними подходящими дробями:

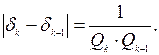
(4)

3). Между подходящими дробями и самой дробью 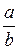справедливы соотношения:

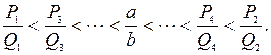
Из этих соотношений видно, что дробь 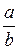всегда заключена между двумя соседними подходящими дробями, интервал между которыми уменьшается по мере возрастания порядка. Этим и объясняется название «подходящие» дроби.