Определяем параметры нагрузки
3. Определяем реактивные сопротивления: индуктивное 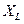 - по формуле (1.19) и емкостное
- по формуле (1.19) и емкостное 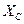 - по формуле (1.20):
- по формуле (1.20):
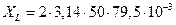
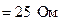 ; (4.8)
; (4.8)
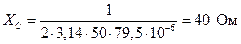 . (4.9)
. (4.9)
4. Определяем полные комплексные сопротивления фаз по формуле (1.21). Из рис. 4.2 видно, что фазы нагрузки 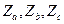 , соединенные «звездой», и фазы нагрузки
, соединенные «звездой», и фазы нагрузки 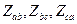 , соединенные «треугольником», образованы одинаковыми элементами. Это позволяет записать
, соединенные «треугольником», образованы одинаковыми элементами. Это позволяет записать
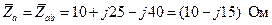 ; (4.10)
; (4.10)
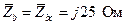 ; (4.11)
; (4.11)
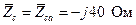 . (4.12)
. (4.12)
5. Определяем полные сопротивления фаз по формуле
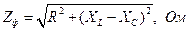 . (4.13)
. (4.13)
Тогда
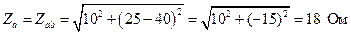 ; (4.14)
; (4.14)
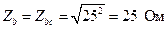 ; (4.15)
; (4.15)
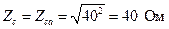 . (4.16)
. (4.16)
6. Определяем угол сдвига между током и напряжением для соответствующих фаз нагрузки по формуле (1.26):
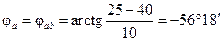 ; (4.17)
; (4.17)
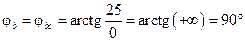 ; (4.18)
; (4.18)
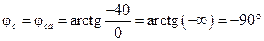 . (4.19)
. (4.19)
Результаты расчета углов сдвига между током и напряжением для соответствующих фаз нагрузки не противоречат данным табл. 1.1.
7. Полное комплексное сопротивление фазы в тригонометрической форме имеет вид
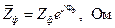 . (4.20)
. (4.20)
Тогда с учетом результатов п.5 и п.6 получим:
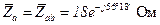 ; (4.21)
; (4.21)
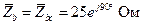 ; (4.22)
; (4.22)
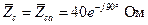 . (4.23)
. (4.23)
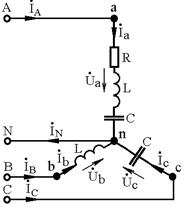 Рис. 4.3 Рис. 4.3
|
Определяем напряжения, токи и полные комплексные мощности фаз для нагрузки, соединенной в «звезду»
8. Выполняем преобразование трехфазной электрической цепи (см. рис. 4.1) для соединения нагрузки «звездой», учитывая, что в соответствующие фазы нагрузки включены элементы, представленные на рис. 4.2. Полученный после преобразования участок трехфазной цепи показан на рис. 4.3. На этом же рисунке показаны условные направления токов и напряжений.
9. Пренебрегая сопротивлением линейных проводов, условимся, что к фазам нагрузки приложены напряжения, равные фазным напряжениям источника.
Тогда в соответствии с (3.14) можем записать:
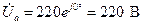 ; (4.24)
; (4.24)
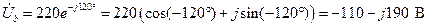 ; (4.25)
; (4.25)
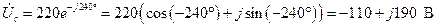 . (4.26)
. (4.26)
10. На основании закона Ома в соответствии с выражениями (3.16)-(3.18) определяем комплексы действующих значений фазных токов:
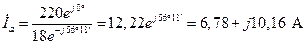 ; (4.27)
; (4.27)
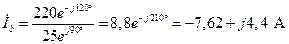 ; (4.28)
; (4.28)
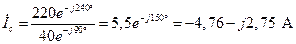 . (4.29)
. (4.29)
Запишем действующие значения фазных токов:
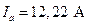 ; (4.30)
; (4.30)
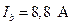 ; (4.31)
; (4.31)
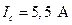 . (4.32)
. (4.32)
11. На основании первого закона Кирхгофа для узла n в соответствии с выражением (3.30) определяем ток в нейтральном проводе:
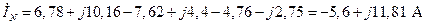 . (4.33)
. (4.33)
Определяем действующее значение тока в нейтральном проводе
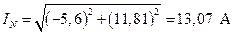 . (4.34)
. (4.34)
12. Совмещенная векторная диаграмма фазных токов и напряжений на комплексной плоскости показана на рис. 4.4. Масштабы: по току 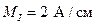 ; по напряжению
; по напряжению 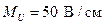 .
.
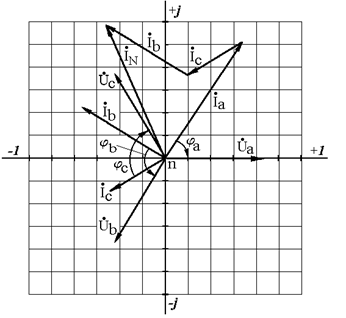
Рис. 4.4
Для нагрузки, фазы которой соединены в «звезду», существует еще один способ решения, основанный на использовании действующих значений напряжений и токов. Рассмотрим методику решения данным способом.
Определяем действующие значения фазных напряжений нагрузки на основании (4.1) с учетом (3.14)
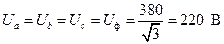 . (4.35)
. (4.35)
Определяем величины полных сопротивлений фаз в соответствии с (4.13):
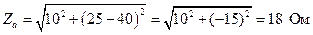 ; (4.36)
; (4.36)
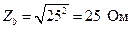 ; (4.37)
; (4.37)
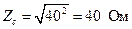 . (4.38)
. (4.38)
На основании закона Ома в соответствии с выражениями (3.16)-(3.18) определяем действующие значения фазных токов
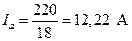 ; (4.39)
; (4.39)
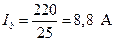 ; (4.40)
; (4.40)
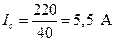 . (4.41)
. (4.41)
При построении векторной диаграммы условимся, что вектор фазного напряжения 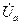 нагрузки совпадает с действительной осью комплексной плоскости. Строим вектор фазного напряжения
нагрузки совпадает с действительной осью комплексной плоскости. Строим вектор фазного напряжения 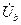 , отстающим от вектора
, отстающим от вектора 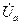 на угол 120о, а вектор фазного напряжения
на угол 120о, а вектор фазного напряжения 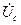 - опережающим вектор
- опережающим вектор 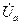 на угол 120о.
на угол 120о.
Чтобы отложить векторы фазных токов, определим угол сдвига между током и напряжением для каждой фазы нагрузки по формуле (1.26):
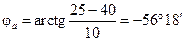 ; (4.42)
; (4.42)
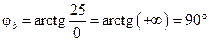 ; (4.43)
; (4.43)
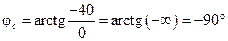 . (4.44)
. (4.44)
В соответствии с выражением (3.30) вектор тока в нейтральном проводе 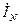 может быть определен как геометрическая сумма векторов фазных токов. Данный прием показан на векторной диаграмме (см. рис. 4.4). Чтобы определить действующее значение тока
может быть определен как геометрическая сумма векторов фазных токов. Данный прием показан на векторной диаграмме (см. рис. 4.4). Чтобы определить действующее значение тока 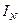 с помощью векторной диаграммы, необходимо умножить длину вектора на масштаб тока.
с помощью векторной диаграммы, необходимо умножить длину вектора на масштаб тока.
Определяем напряжения, токи и активную мощность по методу двух ваттметров для нагрузки, фазы которой соединены «треугольником»
 Рис. 4.5
Рис. 4.5
|
13. Выполняем преобразование трехфазной электрической цепи (см. рис. 4.1) для соединения нагрузки «треугольником», учитывая, что в соответствующие фазы нагрузки включены элементы, представленные на рис. 4.2. Полученный после преобразования участок трехфазной цепи показан на рис. 4.5. На этом же рисунке показаны условные направления токов и напряжений.
14. Пренебрегая сопротивлением линейных проводов, условимся, что к фазам нагрузки приложены напряжения, равные фазным напряжениям источника. Тогда на основании (3.33) можем записать:
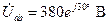 ; (4.45)
; (4.45)
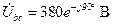 ; (4.46)
; (4.46)
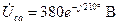 . (4.47)
. (4.47)
15. На основании закона Ома в соответствии с выражениями (3.34)-(3.36) определяем фазные токи:
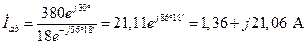 ; (4.48)
; (4.48)
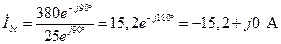 ; (4.49)
; (4.49)
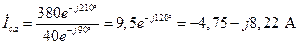 . (4.50)
. (4.50)
16. На основании первого закона Кирхгофа в соответствии с выражениями (3.37)-(3.39) определяем линейные токи:
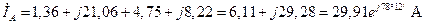 ; (4.51)
; (4.51)
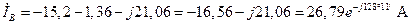 ; (4.52)
; (4.52)
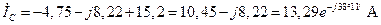 . (4.53)
. (4.53)
17. Согласно выражению (3.29) сумма токов в трехфазной трехпроводной цепи равна нулю. Проверим это:
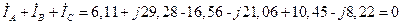 . (4.54)
. (4.54)
Условие (3.29) выполняется, что свидетельствует о правильности расчета.
18. Определяем активную мощность по методу двух ваттметров (рис. 4.5). В соответствии со схемой включения ваттметров можем записать для ваттметра W1:
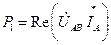 , Вт; (4.55)
, Вт; (4.55)
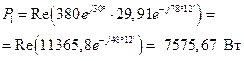 (4.56)
(4.56)
для ваттметра W2:
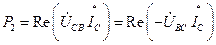 , Вт. (4.57)
, Вт. (4.57)
Из рис. 4.5 и уравнения (4.57) видно, что комплексное напряжение 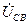 , по величине равно напряжению
, по величине равно напряжению 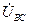 и противоположно ему по направлению. Следовательно,
и противоположно ему по направлению. Следовательно, 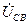 может быть получено разворотом вектора
может быть получено разворотом вектора 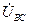 на
на 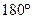 . Тогда, учитывая (4.6), можем записать:
. Тогда, учитывая (4.6), можем записать:
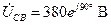 ; (4.58)
; (4.58)
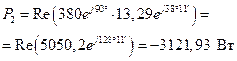 (4.59)
(4.59)
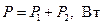 ; (4.60)
; (4.60)
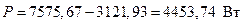 . (4.61)
. (4.61)
19. Совмещенная векторная диаграмма фазных токов и напряжений на комплексной плоскости показана на рис. 4.6. Масштабы: по току 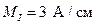 ; по напряжению
; по напряжению 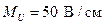 .
.
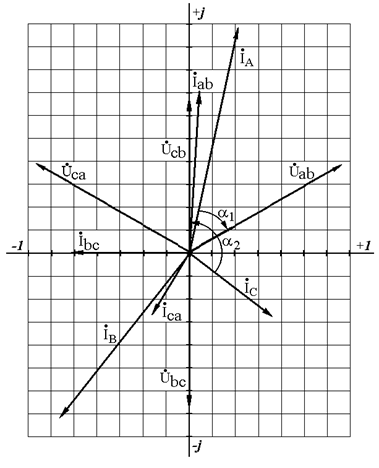
Рис. 4.6
Активную мощность по методу двух ваттметров (см. рис. 4.5) можно определить также с помощью векторной диаграммы по следующим формулам:
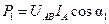 ; (4.62)
; (4.62)
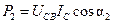 , (4.63)
, (4.63)
где 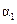 - угол между векторами тока
- угол между векторами тока 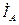 и напряжения
и напряжения 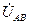 ,
, 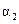 - угол между векторами тока
- угол между векторами тока 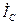 и напряжения
и напряжения 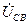 .
.
Для этого на векторной диаграмме необходимо отложить вектор напряжения 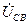 в соответствии с (4.58). Активную мощность, потребляемую от источника фазами «треугольника», определяем по (4.60).
в соответствии с (4.58). Активную мощность, потребляемую от источника фазами «треугольника», определяем по (4.60).
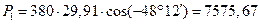 Вт; (4.64)
Вт; (4.64)
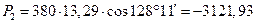 Вт ; (4.65)
Вт ; (4.65)
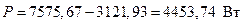 . (4.66)
. (4.66)
4.3. Примерный перечень контрольных вопросов при защите расчетного задания №2
1. Дайте определение трехфазного симметричного источника.
2. Что называют фазой трехфазной цепи?
3. Как нужно соединить начала и концы фаз трехфазного источника, чтобы получить соединение «звездой»?
4. Как нужно соединить начала и концы фаз трехфазного потребителя, чтобы получить соединение «звездой»?
5. Как нужно соединить начала и концы фаз трехфазного потребителя, чтобы получить соединение «треугольником»?
6. Что такое симметричная и несимметричная нагрузка трехфазной цепи?
7. В каком соотношении находятся фазные и линейные напряжения трехфазного симметричного потребителя, фазы которого соединены «звездой»?
8. В каком соотношении находятся фазные и линейные токи трехфазного симметричного потребителя, фазы которого соединены «звездой»?
9. Объясните методику расчета для потребителя, фазы которого соединены «звездой»?
10. Объясните методику построения векторной диаграммы для потребителя, фазы которого соединены «звездой»?
11. Объясните роль нейтрального провода при симметричной и несимметричной нагрузках.
12. В каком соотношении находятся фазные и линейные напряжения трехфазного симметричного потребителя, фазы которого соединены «треугольником»?
13. В каком соотношении находятся фазные и линейные токи трехфазного симметричного потребителя, фазы которого соединены «треугольником»?
14. Объясните методику расчета для потребителя, фазы которого соединены «треугольником»?
15. Объясните методику построения векторной диаграммы для потребителя, фазы которого соединены «треугольником»?
16. Как измеряют активную мощность в трехфазных цепях?
Библиографический список к третьему и четвертому разделам
1. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов. М.: Энергоатомиздат, 2000. С. 104-123.
2. Рекус Г.Г., Белоусов А.И. Сборник задач по электротехнике и основам электроники. М.: Высш. школа, 1991. С. 211-231.
5. ОРГАНИЗАЦИОННЫЕ УКАЗАНИЯ.
ОФОРМЛЕНИЕ И ЗАЩИТА РАСЧЕТНЫX ЗАДАНИЙ
Руководство выполнением расчетных заданий осуществляет лектор потока или преподаватель, ведущий практические и лабораторные занятия в каждой учебной подгруппе. Расчетные задания выдаются по мере изучения тем курса, при этом каждому студенту указывается номер одного из вариантов, приведенных в табл. 2.1 и табл. 2.2 для расчетного задания №1 или в табл. 4.1 и табл. 4.2 для расчетного задания №2. Срок выполнения расчетных заданий определяет руководитель.
Для своевременного и качественного выполнения расчетных заданий студенты обязаны посещать консультации по самостоятельной работе, предусмотренные учебным расписанием, и могут использовать часы консультаций, проводимых лектором.
Оформлять расчетные задания следует на двойных тетрадных листах. Первым листом расчетного задания является титульный лист, образец оформления которого представлен в Приложении. Векторные диаграммы могут быть выполнены на миллиметровой бумаге.
К защите расчетного задания студент должен представить полностью завершенный и оформленный расчет с пояснением используемых формул и проводимых преобразований, содержащий исходные данные, схемы и совмещенные векторные диаграммы с указанием масштабов.
Выполненное и оформленное расчетное задание сдается на проверку руководителю. После проверки производится защита расчетных заданий, проводимая в форме собеседования. По результатам собеседования (с учетом срока сдачи расчетного задания на проверку) студенту выставляется оценка, которая фиксируется в журнале учебной группы и учитывается при подсчете рейтинга.
Приложение
ОБРАЗЕЦ ОФОРМЛЕНИЯ ТИТУЛЬНОГО ЛИСТА
Казанский государственный технологический университет
Кафедра
электротехники и электропривода
РАСЧЕТ РАЗВЕТВЛЕННОЙ ЦЕПИ СИНУСОИДАЛЬНОГО
ПЕРЕМЕННОГО ТОКА МЕТОДОМ КОМПЛЕКСНЫX ЧИСЕЛ
Расчетное задание №1по курсу
Электротехника
Вариант №19
Выполнил студент гр. 89-22 Д.А. Богатырев
Принял доц. Ю.Г. Соколов
2011
СОДЕРЖАНИЕ
Введение 3
1. Расчет электрических цепей синусоидального переменного тока методом комплексных чисел 3
1.1.Понятие о комплексных числах. Комплексная
плоскость 3
1.2.Формы записи комплексных чисел 4
1.3.Действия над комплексными числами 5
1.4. Способы изображения синусоидальных функций времени 6
1.5. Метод комплексных чисел. Законы электрических цепей в комплексной форме 8
1.6.Понятие о полном комплексном сопротивлении 9
1.7.Угол сдвига фаз. Векторная диаграмма 10
1.8.Полная комплексная мощность 15
2. Расчет разветвленной цепи переменного тока методом комплексных чисел 17
2.1. Условие расчетного задания №1. Варианты
заданий 17
2.2. Пример решения расчетного задания №1. Методика расчета. Алгоритмы решения 20
2.3. Примерный перечень контрольных вопросов при защите расчетного задания №1 28
Библиографический список к первому и второму
разделам 29
3. Трехфазные электрические цепи 30
3.1. Трехфазная система питания потребителей
электроэнергии. Расширение понятия «фаза». Расчет
трехфазных цепей 30
3.2. Трехфазные трехпроводные цепи при соединении
фаз нагрузки «звездой» 33
3.3. Трехфазные четырехпроводные цепи при соединении
фаз нагрузки «звездой» 36
3.4. Трехфазные электрические цепи при соединении
фаз нагрузки «треугольником» 38
3.5. Активная, реактивная и полная мощности трехфазной
цепи 40
3.6. Измерение активной мощности в трехфазных цепях 41
4. Расчет трехфазных цепей методом комплексных чисел 44
4.1. Условие расчетного задания №2. Варианты задания 44
4.2. Пример решения расчетного задания №2 47
4.3. Примерный перечень контрольных вопросов
при защите расчетного задания №2 58
Библиографический список к третьему и четвертому разделам 59
5. Организационные указания. Оформление и защита
расчетных заданий 60
Приложение. Образец оформления титульного листа 61
Расчет электрических цепей переменного тока
методом комплексных чисел
Макаров Валерий Геннадьевич
Цвенгер Игорь Геннадьевич
Запускалова Татьяна Александровна
Желонкин Антон Владиславович
Редактор Л. Г. Шевчук
Корректор Ю. Е. Стрыхарь
Лицензия № 020404 от 6.03.97 г.
Подписано в печать 5.09.2001 Формат 60х84 1/16
Бумага писчая Печать RISO 3,72 усл. печ. л.
4,0 уч. изд.л. Тираж 100 экз. Заказ 241 «С» 165
Издательство Казанского государственного
технологического университета
Офсетная лаборатория Казанского государственного
технологического университета
420015, Казань, К. Маркса, 68
Дата добавления: 2015-08-01; просмотров: 1579;
