Способы изображения синусоидальных функций времени
Синусоидальные функции времени могут быть представлены тригонометрической формой записи, временными диаграммами, вращающимися векторами и комплексными числами.
Тригонометрическая форма записи тока, изменяющегося во времени по синусоидальному закону, может быть представлена выражением
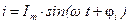, (1.14)
где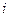 
- мгновенное значение тока; 
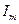- максимальное (амплитудное) значение тока; 
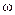- угловая частота, характеризующая скорость изменения фазового угла; 
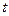- текущее значение времени; 
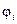- начальная фаза (начальный фазовый угол).
Геометрический смысл параметров, входящих в выражение (1.14), раскрывает временная диаграмма,представленная на рис.1.2 б.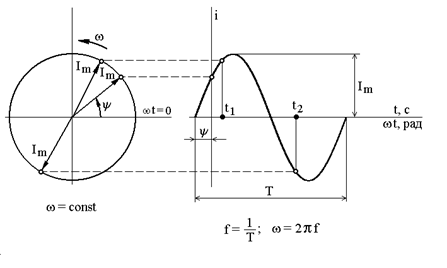 
а б
Рис. 1.2
Переход от временных диаграмм к вращающимся векторам для различных моментов времени показан на рис. 1.2 а, б. Очевидно, что вектор длиной 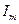вращается с постоянной угловой частотой 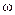. При этом за положительное направление вращения в электротехнике принимается направление против хода часовой стрелки. Проекция вращающегося вектора на ось ординат определяет мгновенное значение синусоидального тока.
В электротехнике, кроме мгновенных и максимальных значений синусоидальных величин, используются средние и действующие значения. Именно эти значения показывают большинство измерительных приборов, поэтому условимся, что далее в расчетах будут использоваться только действующие значениясинусоидальных электродвижущих сил (ЭДС), напряжений и токов.
Действующие значения синусоидальных ЭДС, напряжений и токов могут быть определены на основании максимальных значений с помощью следующих выражений:
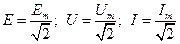. (1.15)
На рис.1.2 а показано, что длина вращающегося вектора равна амплитудному значению синусоидальной величины. Однако следует отметить, что вращающиеся векторы могут иметь длину, равную действующему значению.
1.5. Метод комплексных чисел. Законы электрических цепей в комплексной форме
Метод комплексных чисел нашел широкое применение в электротехнике при расчетах электрических цепей синусоидального переменного тока. При этом в качестве векторов на комплексной плоскости изображаются синусоидальные функции времени (ЭДС, напряжения и токи).
Сущность расчета электрических цепей с помощью данного метода заключается в том, что графические операции над векторами заменяют алгебраическими действиями над комплексными числами.
В электротехнике, чтобы избежать сходства мнимой единицы iс силой тока, мнимую единицу обозначают буквой j.
При использовании метода комплексных чисел уравнения электрических цепей записывают на основании законов Ома и Кирхгофа.
Математическое выражение закона Ома в комплексной форме имеет вид
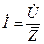, (1.16)
где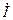 
- комплекс действующего значения силы тока (комплекс тока); 
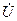- комплекс действующего значения напряжения, приложенного к цепи (комплекс напряжения); 
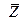- полное комплексное сопротивление.
Отличие обозначения комплексного сопротивления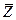 
от обозначения комплексных напряжения 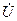и тока 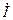связано с тем, что комплексное сопротивление не является синусоидальной функцией времени.
Математическое выражение первого закона Кирхгофа в комплексной форме имеет вид
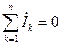, (1.17)
где k – число комплексных токов, сходящихся в узле электрической цепи.
В соответствии с (1.17) сумма комплексных токов, сходящихся в узле электрической цепи, равна нулю.
Математическое выражение второго закона Кирхгофа в комплексной форме имеет вид:
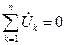, (1.18)
где k – число комплексных напряжений вдоль замкнутого контура.
В соответствии с (1.18) сумма комплексных напряжений вдоль любого замкнутого контура равна нулю.
1.6. Понятие о полном комплексном сопротивлении
Составными элементами цепей синусоидального тока являются активное сопротивление R, индуктивность L и емкость C. Каждый из этих элементов оказывает сопротивление переменному току.
На активном сопротивлении R энергия электрического тока преобразуется в тепловую энергию. Такое преобразование является необратимым.
На индуктивности L происходит периодическое преобразование энергии электрического тока в энергию магнитного поля, накопление и обратное преобразование.
На емкости С происходит периодическое преобразование энергии электрического тока в энергию электрического заряда, накопление и обратное преобразование.
Поскольку процессы в индуктивности и емкости являются обратимыми, то эти элементы называют реактивными.
Индуктивность обладает реактивным сопротивлением, которое называют индуктивным сопротивлением
(1.19)
где f – частота переменного синусоидального напряжения, Гц; L – индуктивность, Гн.
Конденсатор обладает реактивным сопротивлением, которое называют емкостным сопротивлением
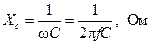(1.20)
где С – емкость, Ф.
Если элементы R, L, C соединены последовательно, то полное комплексное сопротивление можем записать в виде
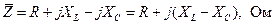. (1.21)
В соответствии с (1.21) очевидно, что полное комплексное сопротивление имеет действительную и мнимую части:
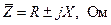(1.22)
где R – активное сопротивление; X – реактивное сопротивление.
В (1.22) знак «плюс» перед 
ставится, если 
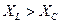, в противном случае ставится знак «минус».
1.7. Угол сдвига фаз. Векторная диаграмма
Токи и напряжения на различных участках электрической цепи синусоидального тока могут не совпадать по фазе, например:
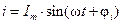; (1.23)
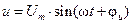, (1.24)
где 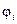- начальная фаза тока; 
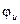- начальная фаза напряжения.
Тогда угол сдвига фаз между током и напряжением определяют как разность их начальных фаз
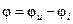. (1.25)
Угол сдвига фаз между током и напряжением на некотором участке электрической цепи зависит от характера сопротивления данного участка и определяется по формуле:
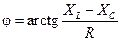. (1.26)
Наглядное представление о фазовом расположении различных векторов дает векторная диаграмма токов и напряжений.
Векторная диаграмма – это совокупность векторов на комплексной плоскости, изображающих синусоидальные функции времени одной и той же частоты и построенных с соблюдением их начальных фаз.
Поскольку расчет электрических цепей синусоидального переменного тока ведется, как правило, с использованием метода комплексных чисел, то и векторные диаграммы также строятся на комплексной плоскости.
Векторные диаграммы чаще всего выполняют совмещенными, то есть на одной комплексной плоскости откладывают векторы токов и напряжений для отдельных участков цепи. При этом необходимо выбрать масштабы для токов и напряжений. Следует отметить, что для токов может быть выбран один масштаб, а для напряжений – другой. Это никоим образом не искажает общей картины, поскольку векторная диаграмма дает представление о взаимном расположении векторов и позволяет судить о наличии сдвига фаз между током и напряжением на отдельных участках электрической цепи.
Из курса высшей математики известно, что над векторами можно производить следующие действия: сложение, вычитание, умножение на число и деление на число.
В электротехнике принято с помощью векторной диаграммы складывать или вычитать векторы. Очевидно, что эти действия можно производить над векторами, имеющими одинаковую размерность.
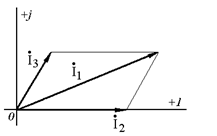
На рис. 1.3 а показано сложение двух комплексных токов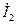 
, 
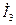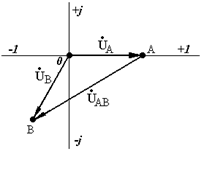
по правилу параллелограмма. Результатом сложения является комплексный ток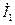 
. На рис. 1.3 б показано вычитание комплексного напряжения 
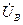из комплексного напряжения 
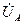, в результате чего получаем комплексное напряжение 
.
| 
|
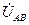а б
Рис. 1.3
Дата добавления: 2015-08-01; просмотров: 789;