Понятие о комплексных числах. Комплексная плоскость

ВВЕДЕНИЕ

Данное пособие предназначено для студентов, изучающих курс «Электротехника», который может быть успешно усвоен, если теоретические знания подкреплены соответствующими расчетными примерами.

Практика показывает, что самостоятельное решение задач по данному курсу не всегда доступно студентам. С учетом этого в пособии рассматриваются примеры решения типовых задач, выполняемых в рамках самостоятельной работы студентов. При этом в каждом примере приводятся основные положения и формулы, облегчающие проведение расчета, а следовательно, и изучение соответствующего раздела.

В пособии рассматриваются примеры решения задач по расчету:

1) разветвленных цепей синусоидального переменного тока;

2) трехфазных цепей.

Следует отметить, что примеры решения задач основываются на использовании метода комплексных чисел.

Сведения, приведенные в пособии, позволяют решать задачи без дополнительного справочного материала.

РАСЧЕТ электрических цепей СинУСОИДАЛЬНОГО

ПЕРЕМЕННОГО ТОКА МЕТОДом КОМПЛЕКСНЫX ЧИСЕЛ

Понятие о комплексных числах. Комплексная плоскость

Из курса высшей математики известно, что число вида

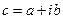, (1.1)

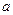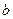где и - любые действительные числа, 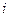- мнимая единица, называется комплексным числом в алгебраической форме.

При этом 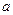является действительной (реальной) частью комплексного числа 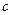и обозначается 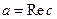, соответственно 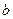является мнимой частью комплексного числа 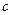и обозначается .

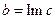Мнимая единица удовлетворяет соотношению

или 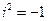. (1.2)

Если 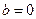, то очевидно, что комплексное число 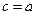является действительным числом; и если 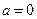, то комплексное число 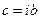является чисто мнимым числом.

Два комплексных числа 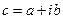и 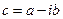, имеющих одинаковые действительные и противоположные мнимые части, называются сопряженными комплексными числами.

Модуль комплексного числа

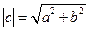(1.3)

и его аргумент

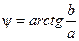. (1.4)

Комплексное число 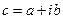можно изобразить точкой 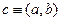или радиус-вектором на комплексной плоскости (рис. 1.1). При этом длина радиус-вектора соответствует модулю комплексного числа, определяемого по формуле (1.3), а угол 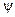между действительной осью комплексной плоскости и радиус-вектором соответствует аргументу комплексного числа, определяемому по формуле (1.4).

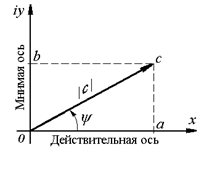
Рис.1.1