Формулировка Максвелла

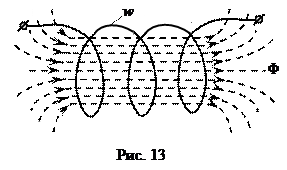Эта формулировка более подходит к ситуации, когда магнитное поле Φ, пронизывающее простой контур или катушку с числом витков w, изменяется во времени. Рассмотрим более сложный случай, когда магнитный поток Φ пронизывает катушку, проходя все ее витки w (рис. 13).

Согласно закону электромагнитной индукции по Максвеллу можно записать

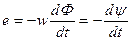где е – индуктированная э.д.с. в вольтах (В);

ψ = wΦ – потокосцепление в веберах (Вб).

Закон по Максвеллу читается следующим образом: индуктированная э.д.с. равна взятой с обратным знаком первой производной от потокосцепления по времени.

Знак минус в формулировке Максвелла позволяет математически точно определить направление индуктированной э.д.с. в соответствии с принципом Ленца.

Принцип Ленца (закон электромагнитной инерции) был сформулирован этим ученым в 1833 году: при изменении магнитного потока в электрической цепи индуктируется э.д.с. такого направления, что вызываемый ею ток стремится воспрепятствовать причине, вызывающей эту э.д.с., то есть изменению магнитного потока.

В формулировке Фарадея знак минус в правой части равенства (21), как правило, не ставится, поскольку более просто направление э.д.с. определяется по правилу правой руки, хотя принцип Ленца там так же соблюдается.

Очевидно – обе формулировки закона электромагнитной индукции являются равнозначными, то есть одна вытекает из другой и наоборот.

Покажем это на примере, представленном на рисунке 14.

Проводник длиной l движется с постоянной скоростью

v = const в плоскости рисунка, пересекая под прямым углом (α = π/2) магнитные линии равномерного неподвижного поля (B = const). Векторы индукции магнитного поля направлены перпендикулярно к плоскости рисунка от наблюдателя (крестики). Предположим, что за отрезок времени Δt проводник переместился на расстояние Δх. Очевидно: скорость перемещения v = Δх / Δt.

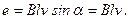
В правой части равенства (23) сделаем подстановки и введем дополнительные обозначения: v = Δх / Δt – скорость; lΔх = Δ(lх) = ΔS – приращение поверхности, пронизываемой магнитным потоком; BΔS = Δ(BS) = ΔΦ – приращение потока. Тогда равенство (23) примет окончательный вид:

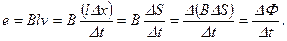
Если подставить в равенство (23а) знак минус, то можно убедиться, что обе формулировки – по Фарадею (23) и по Максвеллу (23а) – вытекают одна из другой, поскольку э.д.с. определяется как скорость изменения магнитного поля относительно электрических контуров или проводников.