РЕАЛЬНЫЕ ГАЗЫ
Модель идеального газа позволяет описывать поведение реальных газов при достаточно высоких температурах и низких давлениях, когда можно пренебречь размерами молекул и их взаимодействием друг с другом. Однако при повышении давления необходимо учитывать, что молекулы не являются материальными точками, а имеют определенный объем. Необходимо учитывать также силы межмолекулярного взаимодействия. Эти силы имеют электромагнитную и квантовую природу. Между молекулами вещества в любом агрегатном состоянии действуют силы взаимного притяжения, проявляющиеся в способности сопротивляться растяжению, образовывать капли и т.д. Кроме того, относительно малая сжимаемость плотных газов и способность жидких и твердых тел сопротивляться сжатию указывает на то, что между молекулами действуют также и силы отталкивания.
 На рис.4.1. приведена качественная зависимость потенциальной энергии взаимодействия молекул от расстояния между ними. Потенциальная энергия равна нулю, когда молекулы находятся далеко друг от друга и силы межмолекулярного взаимодействия не действуют (r → ∞). При постепенном сближении между молекулами появляются силы взаимного притяжения и потенциальная энергия уменьшается, достигая минимума при r = r0. При r < r0 силы отталкивания возрастают и потенциальная энергия также начинает резко возрастать.
На рис.4.1. приведена качественная зависимость потенциальной энергии взаимодействия молекул от расстояния между ними. Потенциальная энергия равна нулю, когда молекулы находятся далеко друг от друга и силы межмолекулярного взаимодействия не действуют (r → ∞). При постепенном сближении между молекулами появляются силы взаимного притяжения и потенциальная энергия уменьшается, достигая минимума при r = r0. При r < r0 силы отталкивания возрастают и потенциальная энергия также начинает резко возрастать.
4.1. Понятие фазы и фазовых переходов. @
Фазой называется совокупность всех частей системы, обладающих одинаковым химическим составом, находящихся в одинаковом состоянии и ограниченных поверхностями раздела. Понятие «фаза» шире, чем понятие «агрегатное состояние». В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по свойствам, составу и строению. Лед, например, встречается более, чем в десяти различных фазах.
Переход вещества из одной фазы в другую называют фазовым переходом. Он всегда связан с качественными изменениями свойств вещества, различают фазовые переходы двух родов. Фазовый переход Ι рода сопровождается поглощением или выделением теплоты, называемой теплотой фазового перехода. Это плавление, кристаллизация и т.п. Фазовые переходы Ι рода характеризуются постоянством температуры (например, температура плавления льда постоянна и равна 0˚С) и сопровождаются изменением объема. Фазовые переходы, не связанные с выделением или поглощением теплоты и изменением объема, называются фазовыми переходами ΙΙ рода. Эти переходы характеризуются скачкообразным изменением теплоемкости (например, переход ферромагнитных веществ в парамагнитное состояние).
Фазовые переходы играют огромную роль в процессах плавления и кристаллизации полимеров при переработке их в изделия. Например, для улучшения физико-механических и диэлектрических свойств некоторые полимеры подвергают вытяжке, в результате чего полимер переходит из аморфного в кристаллическое состояние (фазовый переход I рода). Широкую известность имеют сформированные таким образом полимерные нити – орлон, лавсан и т.д.
4. 2. Уравнение Ван-дер-Ваальса. @
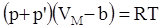 |
Реальные газы с повышением давления и уменьшением температуры уже не подчиняются уравнению Менделеева-Клапейрона. Ван-дер-Ваальс предположил, что в данном уравнении необходимо ввести поправки к объему и давлению. Так как молекулы реального газа имеют собственный объем, то для свободного их перемещения будет предоставлен не весь геометрический объем, занимаемый газом, а меньший - на величину той части объема, которую занимают сами молекулы.. Далее, благодаря силам притяжения молекулы находятся как бы под действием дополнительного давления р’, которое необходимо учитывать вместе с внешним. Скорректированное Ван-дер-Ваальсом уравнение для одного моля реального газа имеет вид:
Расчет показал, что добавочное давление р’= a/VМ2, где a – коэффициент Ван-дер-Ваальса, зависящий только от химической природы газа. Коэффициент b- поправка на собственный объем молекул, равная учетверенному объему молекул,
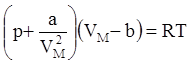 |
находящихся в одном моле. Итак:

Для произвольной массы газа уравнение Ван-дер-Ваальса с учетом равенства VМ = V/ν =VM/m принимает вид:
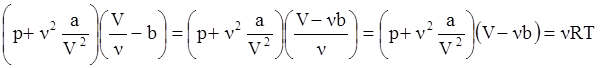 |
где V – это объем всей массы газа.
Если в уравнении Ван-дер-Ваальса для одного моля реального газа раскрыть скобки и привести уравнение к общему знаменателю, то получится уравнение третьей степени относительно VМ при заданных р и Т:
 |
Данное уравнение для конкретного давления р1 может иметь три вещественных корня VМ1, VМ2, VМ3. Зависимости р от VМ, построенные из данного уравнения при различных температурах - это изотермы Ван-дер-Ваальса. (рис.4.2).
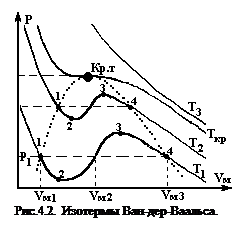 Можно заметить, что пока температура не достигнет некоторого критического значения Ткр, в пространстве (р,V ) имеется область, где каждому значению давления соответствуют три точки изотермы с тремя различными VМ – три корня уравнения Ван-дер-Ваальса. По мере повышения температуры эти три точки сближаются и при Т=Ткр сливаются в одну точку, которая является точкой перегиба критической изотермы. При Т› Ткр изотермы Ван-дер-Ваальса близки к изотермам идеального газа.
Можно заметить, что пока температура не достигнет некоторого критического значения Ткр, в пространстве (р,V ) имеется область, где каждому значению давления соответствуют три точки изотермы с тремя различными VМ – три корня уравнения Ван-дер-Ваальса. По мере повышения температуры эти три точки сближаются и при Т=Ткр сливаются в одну точку, которая является точкой перегиба критической изотермы. При Т› Ткр изотермы Ван-дер-Ваальса близки к изотермам идеального газа.
4. 3. Изотермы реальных газов. @
Английский физик Т.Эндрюс в 1866 г. экспериментально исследовал зависимость молярного объема углекислого газа СО2 от давления при 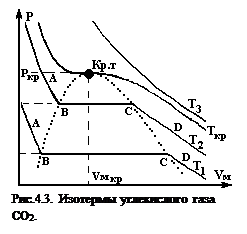 изотермическом сжатии (рис.4.3). Было замечено, что при температурах, меньшей некоторой критической (Ткр=340 К) на изотермах имеется горизонтальный участок В‑С, на котором постоянно давление, а молярный объем возрастает от VВ до VС , причем, чем ниже Т, тем больше разностьVС –VВ. При приближении к Ткр эта разность стремится к нулю. Кривую, снятую при Ткр называют критической изотермой. На ней точки В и С сливаются в одну точку К, называемую критической точкой. Любую “докритическую” изотерму можно разбить на три характерных участка: АВ, ВС и СD. На участках АВ и СD при уменьшении объема давление возрастает, а на участке СВ – не меняется. Это своеобразие докритических изотерм связано с тем, что они охватывают различные агрегатные состояния СО2 : на участке АВ состояние системы характеризуется большой плотностью и малой сжимаемостью, что соответствует жидкости. На участке СD состояние системы характеризуется низкой плотностью и легкой сжимаемостью, что соответствует газообразному состоянию, а на участке ВС углекислота одновременно находится в 2-х агрегатных состояниях – жидком и газообразном. Если мы будем уменьшать объем газа, сжимая его, т.е. двигаться в направлении С →В, то точка С будет соответствовать началу конденсации СО2, а точка В – ее концу. Если же двигаться наоборот, от В к С (изотермическое расширение), то точка В будет соответствовать началу кипения, а точка С – его окончанию. Другими словами, точка В соответствует состоянию кипящей жидкости, а точка С – сухого насыщенного пара. В любой другой точке на участке ВС СО2 представляет собой смесь кипящей жидкости и сухого насыщенного пара. Такую смесь называют влажным паром. Он представляет собой, таким образом, двухфазную систему. С ростом Т прямолинейный участок сокращается по длине, точка В смещается вправо, С – влево. Объясняется это тем, что молярный объем жидкости, находящейся в равновесии с насыщенным паром, увеличивается с ростом температуры, так как при этом в жидкости ослабевают межмолекулярные силы сцепления. Молярный же объем насыщенного пара, напротив, уменьшается. При Т=Ткр, р=ркр, VM=VMкр точки В и С сливаются в одну и газ целиком переходит в жидкость, минуя двухфазное состояние.
изотермическом сжатии (рис.4.3). Было замечено, что при температурах, меньшей некоторой критической (Ткр=340 К) на изотермах имеется горизонтальный участок В‑С, на котором постоянно давление, а молярный объем возрастает от VВ до VС , причем, чем ниже Т, тем больше разностьVС –VВ. При приближении к Ткр эта разность стремится к нулю. Кривую, снятую при Ткр называют критической изотермой. На ней точки В и С сливаются в одну точку К, называемую критической точкой. Любую “докритическую” изотерму можно разбить на три характерных участка: АВ, ВС и СD. На участках АВ и СD при уменьшении объема давление возрастает, а на участке СВ – не меняется. Это своеобразие докритических изотерм связано с тем, что они охватывают различные агрегатные состояния СО2 : на участке АВ состояние системы характеризуется большой плотностью и малой сжимаемостью, что соответствует жидкости. На участке СD состояние системы характеризуется низкой плотностью и легкой сжимаемостью, что соответствует газообразному состоянию, а на участке ВС углекислота одновременно находится в 2-х агрегатных состояниях – жидком и газообразном. Если мы будем уменьшать объем газа, сжимая его, т.е. двигаться в направлении С →В, то точка С будет соответствовать началу конденсации СО2, а точка В – ее концу. Если же двигаться наоборот, от В к С (изотермическое расширение), то точка В будет соответствовать началу кипения, а точка С – его окончанию. Другими словами, точка В соответствует состоянию кипящей жидкости, а точка С – сухого насыщенного пара. В любой другой точке на участке ВС СО2 представляет собой смесь кипящей жидкости и сухого насыщенного пара. Такую смесь называют влажным паром. Он представляет собой, таким образом, двухфазную систему. С ростом Т прямолинейный участок сокращается по длине, точка В смещается вправо, С – влево. Объясняется это тем, что молярный объем жидкости, находящейся в равновесии с насыщенным паром, увеличивается с ростом температуры, так как при этом в жидкости ослабевают межмолекулярные силы сцепления. Молярный же объем насыщенного пара, напротив, уменьшается. При Т=Ткр, р=ркр, VM=VMкр точки В и С сливаются в одну и газ целиком переходит в жидкость, минуя двухфазное состояние.
Из сопоставления изотермы Ван-дер-Ваальса с реальной изотермой Эндрюса вытекает, что они примерно совпадают на участках, отвечающих однофазным состояниям вещества, но ведут себя совершенно различным образом в области расслоения на две фазы. Вместо S-образного завитка на изотерме Ван-дер-Ваальса реальная изотерма имеет в этой области прямолинейный горизонтальный участок.
Оказывается, что при некоторых условиях состояния, соответствующие участкам 1-2 и 3-4 (рис.4.2) могут осуществиться. Правда, они не вполне устойчивы. Такие состояния называются метастабильными. Вещество в состояниях 1-2 называется перегретой жидкостью, вещество в состояниях 3-4 называется пересыщенным (переохлажденным) паром. Участок кривой 2-3 практически воспроизведен быть не может, так как это состояние противоречит условию стабильности системы.
Дата добавления: 2015-08-01; просмотров: 993;
