ОСНОВЫ ТЕРМОДИНАМИКИ

2.1. Внутренняя энергия. @

Важной характеристикой любой термодинамической системы является ее внутренняя энергия – энергия хаотического теплового движения частиц системы - молекул, атомов и энергия их взаимодействия. К внутренней энергии не относится кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях. Внутренняя энергия системы в определенном состоянии не зависит от того, как система пришла в это состояние (т.е. от пути перехода), а определяется только значениями термодинамических параметров в этих состояниях. В термодинамике имеются и другие функции, удовлетворяющие этим условиям, их называют функциями состояния системы. Таким образом, внутренняя энергия – это функция состояния.

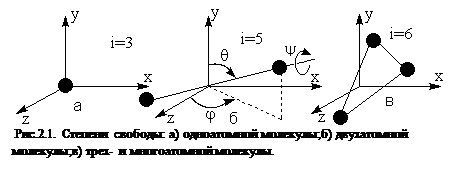
Для дальнейших рассуждений нам понадобится понятие числа степеней свободы – это число независимых переменных (координат), полностью определяющих положение системы в пространстве. Например, молекулу одноатомного газа можно рассматривать как материальную точку, обладающую тремя степенями свободы поступательного движения (координаты x,y,z) (рис.2.1. а). Молекула двухатомного газа, рассматриваемая в классической механике как совокупность двух материальных точек, жестко связанных между собой, имеет уже 5 степеней свободы. У нее имеется 3 степени свободы поступательного движения центра масс и 2 степени вращательного, связанного с поворотами на углы q и j (рис. 2.1. б). Эти углы ‑ полярный угол θ и азимутальный угол φ, определяют ориентацию оси молекулы. В данном случае, на первый взгляд кажется, что необходимо также задавать угол поворота ψ молекулы относительно собственной оси. Но вращение двухатомной молекулы вокруг своей собственной оси ничего не меняет в положении молекулы, так как структуры у материальных точек‑атомов нет и, поэтому, этот угол не нужен для задания положения такой молекулы в пространстве. Трехатомные молекулы (рис. 2.1.в), в которых атомы связаны жестко между собой, имеют 6 степеней свободы, так как здесь уже необходим дополнительный угол ψ.

Если расстояния между атомами меняются, т.е. атомы в молекуле колеблются, то для задания этих расстояний необходимы дополнительные координаты - колебательные степени свободы и общее число степеней свободы будет больше 6. Для много-атомных молекул число степеней может быть намного больше 6.

Ранее мы получили формулу для средней кинетической энергии поступательного движения одно-атомной молекулы идеального газа следующее выражение: ‹ε₀› = 3kT/2. Но у одно-атомной молекулы имеется 3 степени свободы поступательного движения и ни одна не имеет преимущества перед другими. Поэтому на каждую степень в среднем должна приходиться одинаковая энергия, равная 1/3 общей: ‹ε₁› = kT/2. Так как, очевидно, что все степени свободы равноценны, то в классической статистической физике существует закон Больцмана о равномерном распределении энергии по степеням свободы. Он формулируется так: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная кТ/2, а на каждую колебательную степень свободы – кТ. Колебательная степень свободы обладает вдвое большей энергией, так как на нее приходится не только кинетическая, но и потенциальная энергия взаимодействия. Таким образом, средняя энергия любой молекулы ‹ε› = ikT/2, где i - это сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы.

Из этого закона получаем, что внутренняя энергия U_М одного моля идеального газа равна U_М=ikTN_A/2 = iRT/2, а внутренняя энергия U газа массы m равна U = ikTN/2 = iRTm/2M (здесь мы учитываем, что потенциальная энергия взаимодействия молекул равна 0, общее число молекул в одном моле равно N_A, N= mN_A/M и kN_A=R).

2.2. Первое начало термодинамики. @

Обмен энергией между термодинамической системой и внешней средой может осуществляться двумя качественно различными способами: путем совершения работы и путем теплообмена.

Изменение энергии системы, происходящее под действием сил измеряется работой. Если термодинамическая система совершает работу против внешних сил, то работа считается положительной (А>0). Если работу над системой совершают внешние силы, то она считается отрицательной (А< 0).

Изменение энергии системы, происходящее в результате теплообмена, определяется количеством переданной или отнятой теплоты Q. При теплообмене тела систем должны находится в тепловом контакте, т.е. молекулы этих систем должны иметь возможность сталкиваться при своем движении и обмениваться своей кинетической энергией. Если энергия (теплота) передается системе, то Q>0, если она от системы отнимается, то Q<0. Итак, работа и теплота – это две формы передачи энергии от одних тел другим. Поскольку внутренняя энергия - это механическая энергия всех молекул, то при всех ее изменениях должен соблюдаться закон сохранения энергии. Применительно к термодинамическим процессам этим законом является первое начало термодинамики, установленное в результате обобщения опытных данных. Опыт показал, что при любом способе перехода системы из состояния 1 в состояние 2 изменение внутренней энергии системы ΔU = U₁ - U₂ определяется количеством теплоты Q, полученной системой, и работой А, совершенной системой против внешних сил (получаемое тепло увеличивает энергию системы, а работа системы над внешней средой уменьшает ее) :

ΔU = Q – A или Q = ΔU + A

В дифференциальной форме (для малых изменений величин) это запишется следующим образом:

δQ = dU + δA ,

где δQ - бесконечно малое количество теплоты, dU – бесконечно малое изменение внутренней энергии, δA – элементарная работа. Это уравнение выражает первое начало термодинамики: теплота, подводимая к системе, расходуется на изменение ее внутренней энергии и на совершение работы против внешних сил. Знак δ в δQ и δА означают, что данные элементарные приращения не являются полными дифференциалами и, следовательно, А и Q не являются функциями состояния.

Пусть газ заключен в цилиндрический сосуд, закрытый легко скользящим поршнем площадью S. Найдем работу газа при расширении его объема δA = Fdl = pSdl =pdV, где F – сила, с которой газ действует на поршень, dl – перемещение поршня. Если зависимость р(V) изобразить графически, то общая работа при изменении объема от V₁ доV₂ равна площади фигуры, ограниченной кривой р(V), осью абсцисс и прямыми V= V₁ и V= V₂(рис.2.2.). Графически можно изображать лишь равновесные процессы, и все количественные выводы термодинамики строго применимы только к равновесным процессам. При достаточно медленном протекании реальные процессы можно приближенно считать равновесными. Первое начало термодинамики выполняется во всех процессах, связанных с обменом энергией и совершением работы.

2. 3. Теплоемкость. @

Одним из основных свойств тел, которое широко используется в термодинамике, является теплоемкость. Теплоемкостью тела называется физическая величина, численно равная отношению теплоты δQ, сообщаемой телу, к изменению температуры тела в рассматриваемом термодинамическом процессе. Теплоемкость тела зависит от его химического состава, массы и термодинамического состояния, а также от вида процесса, в котором поступает теплота. Тепловые свойства однородных тел характеризуются понятиями удельной и молярной теплоемкостей.

Удельная теплоемкость вещества – величина, численно равная количеству теплоты, необходимому для нагревания единицы массы вещества на 1 Кельвин при данном процессе, единица измерения – Дж/(кг∙К)

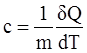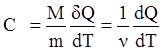Молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания одного моля вещества на 1К , т.е. С =сМ, где М – молярная масса вещества. Теплоемкости одного и того же вещества при разных термодинамических процессах нагревания различаются.

Найдем молярную теплоемкость системы в изобарном процессе, для этого возьмем один моль газа и сообщим ему количество теплоты δQ_М. Согласно определению молярной теплоемкости и первому началу термодинамики можем

записать (здесь δА_М - работа одного моля газа)

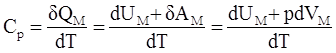Если газ нагревается при постоянном объеме, то dV=0 и δА_М =0. Сообщаемая газу теплота идет только на увеличение его внутренней энергии и теплоемкость для изохорного процесса

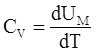Откуда следует, что

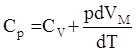Из уравнения Менделеева – Клапейрона для изобарного процесса можно получить pdV_М = RdT. Таким образом, pdV_М /dT = R. Из этой формулы следует физический смысл газовой постоянной: она численно равна работе (δА_М = pdV_М), совершаемой одним молем идеального газа, при его изобарном нагревании на 1 К. После замены получаем:

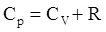Это выражение называется уравнением Майера, оно показывает, что молярная теплоемкость при постоянном давлении С_р всегда больше, чем теплоемкость при постоянном объеме C_v на величину, равную молярной газовой постоянной. Это объясняется тем, что при постоянном объеме все подводимое тепло идет только на увеличение внутренней энергии, т.е. повышение Т, а при постоянном давлении кроме этого требуется еще дополнительное количество теплоты на совершение работы газом против внешних сил при его расширении.

2. 4. Применение первого начала термодинамики к изопроцессам. @

Различают следующие виды термодинамических процессов:

1. Изохорный - это процесс, протекающий при постоянном объеме. V=const. На диаграмме в координатах (р, Т) он изображается прямой, называемой изохорой (рис.2.3.). При изохорном процессе газ не совершает работы над внешними телами, так как dV=0. Вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии и отсюда I начало термодинамики для изохорного процесса δQ = dU. Для одного моля δQ_м=dU_м , где dU_м=С_VdT. Изохорным является процесс сгорания топлива в карбюраторном двигателе.

2. Изобарный – это процесс, протекающий при постоянном давлении. Прямая, изображающая этот процесс в координатах (V,T), называется изобарой (рис.2.4.). Первое начало термодинамики для

изобарного процесса δQ = dU + δA. Так давление не меняется, то работа газа при увеличении объема от V₁ до V₂равна

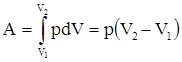Теплота, сообщаемая газу массой m в изобарном процессе

при этом его внутренняя энергия возрастает на величину

так как внутренняя энергия идеального газа не зависит от давления и объема, а определяется лишь температурой. При изобарном нагревании к системе подводится тепло δQ >0 и δA >0, так как газ расширяется. При изобарном сжатии направление процесса меняется на противоположное и теперь тепло отводится от системы, т.е. δQ <0 и δA <0, так как работу над газом совершают внешние силы. dU также будет меньше нуля. Примером изобарного процесса может служить процесс образования пара в паровых котлах или сгорания топлива в воздушно-реактивных двигателях.

3. Изотермический – это процесс, протекающий при постоянной температуре. Кривая, построенная в координатах (р, V), называется изотермой. Она представляет собой гиперболу (рис.2.5.), расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс. Так как при Т = const внутренняя энергия идеального газа не изменяется, то dU = 0 и первое начало термодинамики для изотермического процесса примет вид: δQ = δА. Теплоемкость при изотермическом процессе С_Т=δQ/dT=δQ/0 = ∞ и не имеет смысла. Изотермический процесс осуществляется при наличии термостата (внешней среды или тела с большим запасом внутренней энергии, находящемся при той же температуре).

Найдем работу изотермического расширения газа, учитывая, что все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил и не изменяет его температуру. Учитывая формулу для работы и уравнение Менделеева-Клайперона, получаем

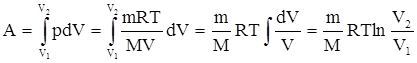Примерами изотермических процессов являются закалка и отжиг сталей в процессе их изготовления. Существуют автомобили и вагоны – рефрижераторы, служащие для перевозки скоропортящихся продуктов. Они имеют теплоизолированный кузов и холодильники для поддержания внутри постоянной температуры и поэтому процесс перевозки продуктов в таких условиях можно назвать изотермическим..

4. Адиабатический процесс. Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой, т.е. δQ = 0, Q = const. Так как δQ = 0, первое начало термодинамики имеет вид: δА=-dU т.е. работа совершается за счет внутренней энергии газа. Если газ расширяется, то δА>0, dU<0 и температура газа уменьшается. Если происходит сжатие газа, то δА<0 и dU>0. Работу над газом совершают внешние силы, внутренняя энергия (а, значит, и температура) газа повышается. Реализовать адибатический процесс можно, если проводить его либо при хорошей теплоизоляции от окружающей среды, либо быстро за короткое время, при котором теплообмен будет мал.

Пуассона или показатель адиабаты. Уравнение адиабатического процесса (уравнение Пуассона) имеет вид: рV^γ= const, где γ = С_р /C_v – коэффициент (показатель адиабаты).

Диаграмма адиабатического процесса (адиабата) в координатах (р,V) изображается гиперболой, более крутой, чем изотерма (рис.2.6.). Объясняется это тем, что при адиабатном сжатии увеличение давления происходит не только за счет уменьшения объема, как при изотермическом сжатии, но также связано с возрастанием температуры. Согласно уравнению р = nkT =NkT/V давление пропорционально T/V и в случае адиабатического сжатия его возрастание определяется одновременно и возрастанием температуры, и уменьшением объема. При адиабатном расширении газа его температура уменьшается и давление падает быстрее, чем при соответствующем изотермическом расширении, поскольку давление уменьшается пропорционально T/V и его падение определяется одновременно и понижением температуры, и увеличением объема. Теплоемкость при адиабатическом процессе С_Q= dQ/ΔT=0/ΔT=0, не имеет большого смысла. Адиабатические процессы широко распространены в технике, например, в двигателях внутреннего сгорания. Истечение газов через сопла реактивных двигателей также может считаться адиабатическим процессом, поскольку происходит очень быстро. Отчетливо выражен адиабатический характер процесса сжатия в дизеле, который не имеет зажигания: адиабатическое нагревание смеси при сжатии приводит к ее самовоспламенению. И, наконец, самый простой бытовой пример: сифон для газирования воды – в момент прокола газового баллончика, когда газ мгновенно его покидает, сам баллончик резко охлаждается (покрывается инеем).

2.5. Второе начало термодинамики. @

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, а в окружающей среде и в системе при этом не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Если система, пройдя через ряд состояний, возвращается в исходное, то такой процесс называется круговым процессом, или циклом. Циклы лежат в основе работы всех тепловых машин – двигателей внутреннего сгорания, паровых и газовых турбин, холодильников. На диаграмме процессов в координатах (р,V) цикл изображается замкнутой кривой, где процесс 1-2 – процесс расширения газа, а 2-1 – процесс сжатия (рис. 2.7.). В результате кругового процесса система может теплоту как получать, так и отдавать. Обозначим полученное количество теплоты Q₁, а отданное - Q₂. Работа, совершаемая газом за цикл, определяется площадью фигуры, ограниченной кривой 1-2-1. В результате цикла система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю, а работа, совершаемая за цикл, равна полученной теплоте Q = Q₁‑ Q₂= А.

2. 6. Энтропия. @

Для описания термодинамических процессов одного первого начала термодинамики недостаточно, потому что оно не позволяет определять направление протекания процессов. Например, процесс самопроизвольной передачи теплоты от холодного тела горячему первым началом не запрещен, однако опыты показывают, что он не происходит. Итак, необходимо определить условия, при которых возможны превращения энергии из одного вида в другой, что позволило бы узнать направления протекания процессов.

В термодинамике, кроме внутренней энергии, существует еще несколько функций состояния системы. Особое место среди них занимает энтропия S. Энтропия как раз и является той величиной, которая позволяет прогнозировать возможность и направление протекания процессов. Энтропия (от греч.entropia–поворот, превращение)- понятие, впервые введенное в термодинамике для определения меры необратимого рассеяния энергии немецким физиком Р.Клаузиусом в 1865г.

Пусть δQ – элементарное количество теплоты, сообщаемое системе каким-либо нагревателем с постоянной температурой Т. Если процесс равновесный (обратимый), то температура системы тоже равна Т. Отношение δQ/Т называется приведенным количеством теплоты и равно изменению энтропии при обратимом процессе: δQ/Т = dS. Поскольку Т всегда > 0, из 2-ого начала видно, что δQ и dS имеют один и тот же знак. Это позволяет по характеру изменения энтропии судить о направлении процесса теплообмена и прогнозировать его возможность. При нагревании тела δQ > 0 и его энтропия возрастает (dS > 0), при охлаждении энтропия убывает. Если δQ=0 (обратимый адиабатический процесс), то dS = 0 и S = const, то есть энтропия остается постоянной.

Энтропия, подобно внутренней энергии, является функцией состояния системы. Энтропия системы равна сумме энтропий всех тел, входящих в систему. Для изолированной системы энтропия в любом обратимом процессе не изменяется и S = const. В термодинамике доказывается, что в необратимом процессе энтропия системы может только возрастать: dS 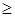0. Объединяя два последних условия, мы получаем, что энтропия замкнутой системы может либо возрастать, либо оставаться постоянной: dS ≥ 0. Это неравенство Клаузиуса также является формулировкой второго начала термодинамики.

С точки зрения молекулярной физики, энтропия является мерой разупорядоченности системы, т.е. чем система более хаотична, тем ее энтропия выше. С этой точки зрения второе начало термодинамики утверждает, что в замкнутой системе, при отсутствии внешних воздействий любая система стремится перейти в состоянии максимальной разупорядоченности. Такое состояние является наиболее вероятным, поэтому энтропию S можно связать с вероятностью W состояния системы соотношением Больцмана S=k lnW, а второе начало объяснять стремлением системы находиться в наиболее вероятном состоянии. Явление увеличения беспорядка можно легко наблюдать при добавлении в воду капли туши. Если не воздействовать на такую систему извне, то через небольшое время тушь полностью перемешается с водой, обратный процесс – процесс собирания частичек туши в каплю, хотя в принципе он и возможен, никогда не наблюдается.

<1 2 345 6 7 >

Дата добавления: 2015-08-01; просмотров: 1810;