Пример 4. Пример решения задачи линейного программирования с помощью Excel
Хозяйство специализируется в полеводстве на производстве зерна, сахарной свеклы и подсолнечника. В с.-х. предприятии имеются 3200га пашни, трудовые ресурсы в объеме 7000чел.-дней и минеральные удобрения в объеме 15000ц.д.в. Требуется найти такое сочетание посевных площадей, которое обеспечило бы получение максимума прибыли.
Следует также учесть, что
- площадь посева технических культур (сахарной свеклы и подсолнечника) не должна превышать 25% общей площади пашни;
- хозяйством заключен договор на продажу зерна в объеме 65000ц.
Для разработки экономико-математической модели необходима подготовка входной информации таблица 5.
Таблица 5.
| Показатели | Сельскохозяйственные культуры | ||
| зерновые | сахарная свекла | подсолнечник | |
| Урожайность, ц/га | |||
| Цена реализации 1 ц продукции, руб./ц. | |||
| Стоимость товарной продукции с 1 га, тыс. руб. | 5,59 | 20,62 | 6,73 |
| Затраты на 1 га: МДС, тыс. руб. | 2,7 | 12,7 | 3,1 |
| труда, чел.-дней. | 1,5 | 4,5 | 1,5 |
| минеральных удобрений, ц.д.в. | 2,3 | ||
| Прибыль с 1 га, руб. | 2,89 | 7,93 | 3,63 |
За неизвестные примем площади посева сельскохозяйственных культур по видам:
- X1 – зерновых культур;
- X2 – сахарной свеклы;
- X3 – подсолнечника.
Для построения экономико-математической модели задачи необходимо учесть все условия. В данном случае, по этим условиям можно составить пять ограничений:
1. сумма площадей посева сельскохозяйственных культур не должна превышать площади, имеющейся в хозяйстве (3200га). Коэффициентами при неизвестных в этом ограничении характеризуют расход пашни на 1га каждой сельскохозяйственной культуры. В данном случае технико-экономические коэффициенты по неизвестным будут равняться единице. В правой части записывается общая площадь пашни.
Х1+Х2+Х3<=3200
2. Сумма площадей посева технических культур не должна превышать площади, которая может быть отведена для этой цели (3200*0,25 = 800га). Коэффициентами при неизвестных в этом ограничении характеризуют расход пашни, отведенной под посевы технических культур, на 1га каждой технической сельскохозяйственной культуры. В данном случае технико-экономические коэффициенты по неизвестным Х2 и Х3 будут равняться единице, а по нетехническим сельскохозяйственным культурам (Х3) – нулю. В правой части записывается максимальная площадь пашни, которая может быть отведена под посевы технических культур.
Х2+Х3<=800
3. Третье и четвертое ограничения гарантируют, что использование трудовых ресурсов и минеральных удобрений не превысит их наличие в хозяйстве. Другими словами, сумма произведений норм затрат ресурсов на 1га на площади посева соответствующих сельскохозяйственных культур не должна превышать объемов ресурсов, имеющихся в с.-х. предприятии. Коэффициентами при неизвестных в этих ограничениях будут являться нормы расхода ресурсов (в третьем ограничении – трудовых ресурсов, в четвертом – минеральных удобрений) на 1га площади посева сельскохозяйственных культур. В данном случае технико-экономические коэффициенты взяты из таблицы 1. В правой части записывается наличие этих ресурсов в хозяйстве.
1,5Х1+4,5Х2+1,5Х3<=7000
2Х1+15Х2+2,3Х3<=15000
4. пятое ограничение гарантирует производство запланированного объема зерна. В качестве коэффициентов при переменных выступает выход зерна с 1га площади посева с.-х. культур. При неизвестной Х1 это урожайность зерновых (таблица 1). При переменных Х2 и Х3 этот коэффициент равен нулю. В правой части записывается план производства зерна.
26Х1>=65000
В результате получена система пяти линейных неравенств с тремя неизвестными. Требуется найти такие неотрицательные значения этих неизвестных Х1 >= 0; Х2 >= 0; Х3 >= 0, которые бы удовлетворяли данной системе неравенств и обеспечивали получение максимума прибыли от отрасли растениеводства в целом:
Zmax = 2,89Х1 + 7,93Х2 + 3,53Х3.
В качестве коэффициентов при неизвестных в целевой функции выступает прибыль, получаемая с 1га площади посева сельскохозяйственных культур. Эти коэффициенты рассчитаны на основании данных таблицы 1.
Поскольку данная задача решается с помощью MS Excel, то и подготовку всей входной информации для построения экономико-математической модели целесообразно осуществлять также с использованием этого табличного процессора рисунок 300. Это облегчает не только расчеты технико-экономических коэффициентов и других данных, но и дает в дальнейшем возможность автоматического обновления информации в экономико-математической модели.
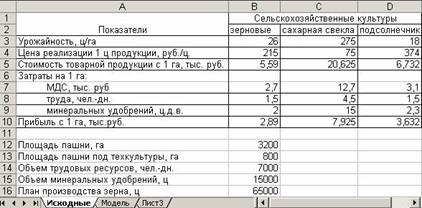
Рисунок 300
Вся разработанная информация сводится в развернутую экономико-математическую модель и заносится в рабочий лист Excel рисунок 301.
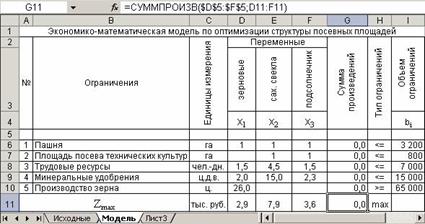
Рисунок 301
Данные в модель рекомендуется заносить в виде ссылок на ячейки с соответствующей информацией в расчетных рабочих листах или рабочих листах с исходными сведениями. На рисунке 302 показано, как в ячейке F9представлена информация по норме затрат удобрений на 1га посева подсолнечника.

Рисунок 302
В столбцы А («№»), В («Ограничения»), С («Единицы измерения») и H («Тип ограничений») вводятся соответствующие данные непосредственно в модель (рис. 99). Они не используются в расчетах и служат для информативности и облегчения понимания содержания модели. В столбец I(«Объем ограничений») вводятся ссылки на ячейки, содержащие соответствующую названию столбца информацию (значения правых частей построенных ранее неравенств).
Для искомых величин переменных Х1, Х2, Х3 были оставлены пустые ячейки – соответственно D5, E5, F5. Изначально пустые ячейки программа Excel воспринимает как ячейки, значение которых равно нулю. Столбец G, названный «Сумма произведений», предназначен для определения суммы произведений значений искомых неизвестных (ячейки D5, E5, F5) и технико-экономических коэффициентов по соответствующим ограничениям (строки 6-10) и целевой функции (строка 11). Таким образом, в столбце G определяется:
- количество используемых ресурсов (ячейка G6 – общей площади пашни; G7 – пашни, которая может быть использована под посевы технических культур; G8 – трудовых ресурсов; G9 – минеральных удобрений);
- количество произведенного зерна (ячейка G10);
- величина прибыли (ячейка G11).
На рисунке 99 показано, как в ячейке G11реализуется запись суммы произведений значений переменных (площадей посева с.-х. культур – ячейки D5, E5, F5) на соответствующие прибыли с 1га их посева(ячейки D11, E11, F11)с помощью функции Excel «СУММПРОИЗВ». Так как при написании данной формулы использованы абсолютные адресации на ячейки от D5до F5,эта формула может быть скопирована в другие ячейки от G6до G10.
Таким образом, построен опорный план (рис. 99) и получено первое допустимое решение. Значения неизвестных Х1, Х2, Х3 равны нулю (ячейки D5, E5, F5–пустые ячейки), ячейки столбца G «Сумма произведений» по всем ограничениям (строкам 6-10) и целевой строке (строка 11) также имеют нулевые значения.
Экономическая интерпретация первого опорного плана звучит следующим образом: в хозяйстве имеются ресурсы, рассчитаны все технико-экономические коэффициенты, но процесс производства еще не начат; ресурсы не использовались, и, соответственно, прибыли нет.
Для оптимизации имеющегося плана воспользуемся инструментом Поиск решения, который находится в меню Сервис. Если нет такой команды в меню Сервис, необходимо в пункте Надстройка поставить галочку напротив Поиск решения. После этого данная процедура станет доступной в меню Сервис.
После выбора данной команды появится диалоговое окно рисунок 303.
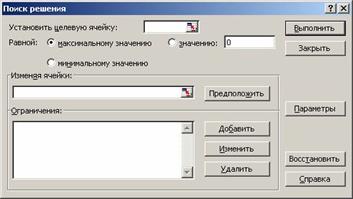
Рисунок 303
Поскольку в качестве критерия оптимизации нами выбрана максимизация прибыли, в поле Установить целевую ячейку введите ссылку на ячейку, содержащую формулу расчета прибыли. В нашем случае это ячейка $G$11. Чтобы максимизировать значение конечной ячейки путем изменения значений влияющих ячеек (влияющими, в данном случае это и изменяемые ячейки, являются ячейки, которые предназначены для хранения значений искомых неизвестных), переключатель установите в положение максимальному значению;
В поле Изменяя ячейки введите ссылки на изменяемые ячейки, разделяя их запятыми; либо, если ячейки находятся рядом, указывая первую и последнюю ячейку, разделяя их двоеточием ($D$5:$F$5).
В поле Ограничения введите все ограничения, накладываемые на поиск решения. Добавление ограничения рассмотрим на примере добавления первого ограничения по общей площади пашни.
В разделе Ограничения диалогового окна Поиск решения нажмите кнопку Добавить. Появится следующее диалоговое окно рисунок 304
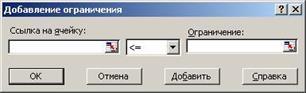
Рисунок 304
В поле Ссылка на ячейку введите адрес ячейки, на значение которой накладываются ограничения. В нашем случае, это ячейка $G$6, где находится формула расчета используемой пашни в текущем плане.
Выберите из раскрывающегося списка условный оператор <=, который должен располагаться между ссылкой и ограничением.
В поле Ограничение введите ссылку на ячейку, в которой находится значение наличия площади пашни в хозяйстве, либо ссылка на это значение. В нашем случае, это ячейка $I$6.
В результате диалоговое окно примет следующий вид рисунок 305.

Рисунок 305
Чтобы принять ограничение и приступить к вводу нового, нажмите кнопку Добавить. Аналогично вводятся и другие ограничения. Чтобы вернуться в диалоговое окно Поиск решения, нажмите кнопку OK.
После выполнения вышеперечисленных инструкций диалоговое окно Поиск решениябудет иметь следующий вид рисунок 306.
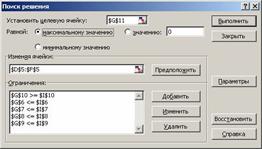
Рисунок 306
Для изменения и удаления ограничений в списке Ограничения диалогового окна Поиск решения укажите ограничение, которое требуется изменить или удалить. Выберите команду Изменить и внесите изменения либо нажмите кнопку Удалить.
Флажок Линейная модель в диалоговом окне Параметры Поиска решения рисунок 307 позволяет задать любое количество ограничений. Флажок Неотрицательные значения позволит соблюсти условие неотрицательности переменных (при решении нашей задачи – поставить обязательно). Остальные параметры можно оставить без изменений, либо установить нужные для вас параметры, при необходимости используя справку.
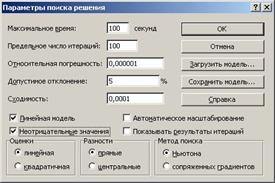
Рисунок 307
Для запуска задачи на решение нажмите кнопку Выполнить и выполните одно из следующих действий:
- чтобы сохранить найденное решение на листе, выберите в диалоговом окне Результаты поиска решения вариант Сохранить найденное решение рисунок 308;
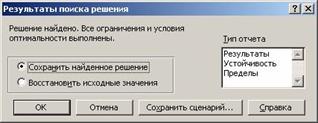
Рисунок 308
- чтобы восстановить исходные данные, выберите вариант Восстановить исходные значения.
Для того чтобы прервать поиск решения, нажмите клавишу ESC.
Лист Microsoft Excel будет пересчитан с учетом найденных значений влияющих ячеек. В результате решения и сохранения результатов поиска на листе модель примет следующий вид рисунок 309.
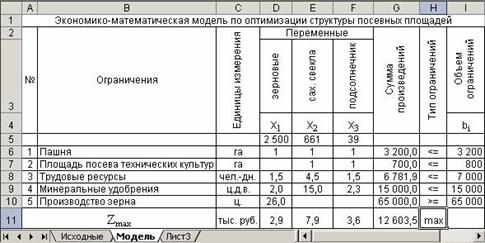
Рисунок 309
В ячейках D5-F5получены значения искомых неизвестных (площади посева равны: зерновых -2500га, сахарной свеклы - 661га, подсолнечника – 39га), в ячейках G6-G9 определены объемы используемых ресурсов (общей площади пашни – 3200га; площади пашни, которая может быть использована под посевы технических культур – 700га; трудовых – 6781,9чел.-дней; минеральных удобрений – 15000ц.д.в.), в ячейке G10 установлено количество произведенного зерна (65000ц). При всех этих значениях величина прибыли достигает 12603,5 тыс. руб. (ячейка G11).
В случае если в результате поиска не было найдено решение, удовлетворяющее заданным условиям, в диалоговом окне Результаты поиска решенияпоявится соответствующее сообщение показанное на рисунке 310.
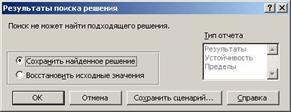
Рисунок 310
Одной из наиболее часто встречающихся причин невозможности найти оптимальное решение является такая ситуация, когда в результате решения задачи выясняется, что имеются ограничения, которые не выполняются. Сохранив найденное решение на листе, требуется построчно сравнить полученные значения столбцов «Сумма произведений» и «Объем ограничений» и проверить, удовлетворяет ли отношение между ними ограничению, стоящему в столбце «Тип ограничений». Найдя, таким образом, невыполняемые ограничения необходимо найти и ликвидировать причины, обуславливающие невозможность соблюдения данного конкретного условия (это может быть, например, слишком большие или, наоборот, очень маленькие запланированные объемы ограничений и т.п.).
Если ограничений в модели очень много, то визуально достаточно трудно сравнивать и проверять на верность каждую строку. Для облегчения рекомендуется добавить в модель еще один столбец «Проверка», где с помощью функций Excel «ЕСЛИ» и «ОКРУГЛ» можно организовать автоматическую проверку рисунок 311.
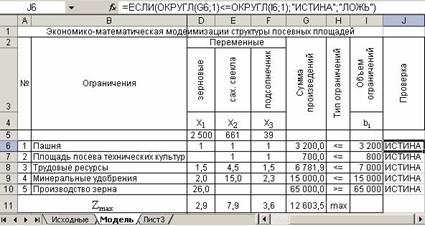
Рисунок 311
Дата добавления: 2015-08-01; просмотров: 1155;
