Первичная статистическая обработка.

5. Парная корреляция. Строится корреляционное поле – график, где на оси абсцисс откладывают значения х, по оси ординат – y. По расположению точек, их концентрации в определенном направлении можно судить о наличии связи.

Для количественной оценки тесноты связи широко используют линейный коэффициент корреляции:

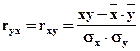[-1; + 1].

Принято считать, что если: r < 0,30 – связь слабая; r = 0,3÷0,7– средняя; при r > 0,70 – сильная, или тесная. Когда r = 1 – связь функциональная. Если же r принимает значение около 0, то это дает основание говорить об отсутствии линейной связи между y и x.

Получив оценки корреляции и регрессии, необходимо проверить их на соответствие истинным параметрам взаимосвязи:

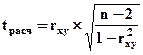, где: t_расч – так называемое расчетное значение t-критерия.

Если t_расч больше теоретического (табличного) значения критерия Стьюдента (t_табл) для заданного уровня вероятности и (n – 2) степеней свободы, то можно утверждать, что r_xy значимо.

Если связь криволинейная r определяют:

1. Корреляционное отношение .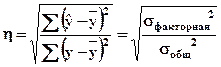

2. Индекс корреляции .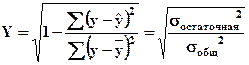

Для выявления существенности связи используют F-критерий Фишера.

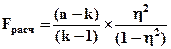, если F_расч ≥ F_табл – связь существенна.

6. Простая регрессия – закономерность, выявленная между y и каждым фактором, влияющим на него.

Выбирается модель, которая точно отображает ряд распределения:

– y= a ± bx, где: a –неучтенные факторы;

– y = a + bx + cx² – рост с ускорением;

– y = a + b/x – гипербола (затухающий процесс).

Параметры находятся по МНК;

– y = ax^b – степенная;

– y = a ´ b^x – показательная;

– y = e^{a + bx} – экстрапоненциальное;

Выбирается аппроксимирующее уравнение, где ошибка наименьшая: .

Аппроксимирующее уравнение проверяется на типичность: ошибки по параметрам m_a, m_b, m_c сравниваются с табличными. Если нетипичны уравнение нельзя использовать в практических целях.

7. Проверка на мультиколлениарность. Необходимо рассчитать r между факторами:

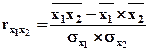, если > 0,6 факторы коллинеарны, выбирается тот, у кот r между ним и y больше.

8. Модель множественной регресии: Y = a + bx₁ + cx₂ + … + zx_n.

Параметры находятся на основе симплекс метода.

9.Расчет совокупного r: .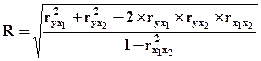

На основе рассчитывается коэффициент детерминации D = R² – если > 0,8 модель можно использовать для практических целей.