Прогнозирование социально-экономических явлений на основе рядов динамики

Ряды динамики – статистические данные, отображающие развитие во времени изучаемого явления. Их также называют динамическими рядами, временными рядами.

Временной ряд – последовательность чисел, которая является значениями некоторого протекающего во времени процесса, причем его значение регистрируются через равные промежутки времени.

В каждом ряду динамики имеется два основных элемента:

1) показатель времени – t;

2) соответствующие им уровни развития изучаемого явления – y;

В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты), либо отдельные периоды (годы, кварталы, месяцы, сутки).

Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.

В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные.

Моментные ряды динамикиотображают состояние изучаемых явлений на определенные даты (моменты) времени.

Интервальные ряды динамики отражают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.

Всякий ряд динамики теоретически может быть представлен в виде составляющих:

1) тренд – основная тенденция развития динамического ряда (к увеличению или снижению его уровней);

2) циклические (периодические колебания, в том числе сезонные);

3) случайные колебания.

При анализе ВР описываются характеристики особенностей ряда, подбор моделей, прогноз, управление поведением ряда.

Этапы анализа:

1. Графическое представление и описание ВР.

2. Выделение и удалении закономерных составляющих ВР (тренд, сезонная, циклическая и случайная компоненты, интервенция).

3. Прогнозирование.

1. Графически оценивается вид тренда, затем гипотеза проверяется на значимость.

Для оценки тренда используют метод наименьших квадратов, он заключается в подборе функции, описывающий временной ряд такой, чтобы:

.

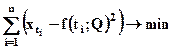Метода скользящих средних. Прогноз любого периода получается как среднее по некоторому фиксированному числу значений временного ряда. Если в ряде нет сезонной составляющей используют 3, 5-точечное сглаживание. 2m + 1 интервал по которому идет скольжение по ряду.

.

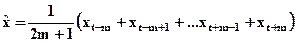Недостатком являются возможные искажения и неправильно подбираются остальные компоненты.

Экспоненциальное сглаживание. Экспоненциальная средняя по t (Q_t) является параметром ассиметричной скользящей средней, в которой учитывается степень старения данных. Используется для прогнозирования временных рядов, имеющих случайное изменение уровня и угла наклона.

,

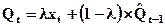где: λ – сглаживающая константа [0;1]

Медианное сглаживание для ВР, имеющих нехарактерные выбросы значений.

Например: 25, 26, 28, 102, 27 – выбираем 27 как среднее значение.

2. X_t – T (оценочное значение тренда) = остатки.

По значениям остатков строится график.

При наличии циклических колебаний используют сглаживание: X_t – T – C.

Наличие сезонности, бывает 2 видов:

– с примерно одинаковыми отклонениями от тренда в каждый сезон (аддитивная модель)

– с увеличением размаха отклонения (мультипликативная).

Если определить сезонность не удается – используют 2 модели и наиболее адекватную ищут с помощью приемов верификации (дополнит проверка значимости прогноза). Если сезонность однозначно не просматривается надо построить спектрограмму или периодограмму (наличие сезонности предполагает резкий пик).

3. Специальная группа методов автопрогнозирования ARIMA(p.d.q) (автокорреляция и проинтегрированная скользящая средняя). p – порядок автокорреляции, d – порядок разницы, q – порядок скользящей средней.

Рассматривается для целей автопрогнозирования поведения стационарных рядов (ряд, в котором распределение случайной величины неизменно во времени). Чтобы получить стационарный ряд надо удалить все детерминированные составляющие. Для определения стационарности строится коррелограмма. Если ряд нестационарен переходят к разности 1-го порядка и т.д. Когда ряд стал стационарен выбираются порядки p, q с наименьшей ошибкой Ms и прогноз строится в доверительном интервале.

В целом различают три группы СЭП:

1. Экспертные оценки

2. Экстраполирование – продолжение в будущем сложившихся тенденций рассматриваемых объектов (анализ врем рядов и прогнозирования).

3. Аналитическое моделирование – исследование процесса на основе построения и использования модели, отражающие внутренние и внешние взаимосвязи в ходе развития (модели роста, балансовые модели, оптимизационные).

Также существуют барометрические методы – прогнозирование избранных временных рядов, кот в сочетании друг с другом указывают направление развития исследуемого процесса.