Уравнение неразрывности в дифференциальной форме
В потоках несжимаемой жидкости, в которых нет ни оттока, ни присоединения расхода, объемный расход в любом сечении постоянный. Можно поэтому предположить, что в каждой точке внутри потока должно выполняться соотношение, гарантирующее, что в ней не происходит ни исчезновения, ни возникновения жидкости. Таким уравнением является уравнение неразрывности в дифференциальной форме. Если поток в каждой точке задан вектором скорости 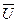 (x,y,z) (в проекциях
(x,y,z) (в проекциях 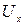 ,
, 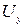 и
и 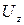 ), то уравнение неразрывности имеет вид
), то уравнение неразрывности имеет вид
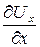 +
+ 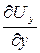 +
+ 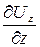 = 0.
= 0.
Уравнение неразрывности должно выполняться в каждой точке потока жидкости.
Задача 6.3.Скорость потока задана так
Ux = a (3x – 2y - z), Uy = a (3x – 2y – 2z), Uz = a (2x – 3y – z).
Проверить, возможно ли существование такого потока. В выражениях для Ux,Uy и Uz постоянный коэффициент a служит для сохранения размерности скорости в правой части.
Решение.Подсчитаем частные производные:
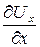 = 3a;
= 3a; 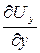 = - 2a;
= - 2a; 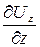 = - a.
= - a.
Складывая их, получаем ноль, поэтому уравнение неразрывности выполняется и такой поток может существовать.
Дата добавления: 2015-08-01; просмотров: 1921;
