Подобие

Различают геометрическое, кинематическое и динамическое подобие потоков; совокупность их составляет механическое подобие потоков жидкости.

Геометрическое подобие состоит в том, что все сходственные линейные элементы двух подобных потоков пропорциональны, а соответствующие углы равны. При этом отношение сходственных линейных размеров натуры L_H и модели L_M одинаково для всех размеров

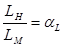где α_L – линейный масштаб.

Сходственные площади и объемы также находятся в одном и том же соотношении

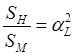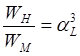Одного геометрического подобия недостаточно для того, чтобы модель правильно отражала работу натурного сооружения или потока. Например, движение жидкости в двух геометрически подобных трубах может иметь различный характер – в одной ламинарный, а в другой – турбулентный.

Кинематическое подобие состоит в том, что в сходственных точках все кинематические параметры находятся в одинаковом отношении, причем векторные величины имеют соответственно одинаковые направления. Во всех сходственных точках для линейной скорости имеем

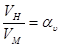так же как и для линейного ускорения

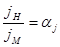Время прохождения сходственными частицами сходственных расстояний находится (как следствие (2.3) и (2.4)) также в одном и том же соотношении

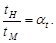
Картины линий тока на натуре и на модели будут по виду тождественны. Условия (2.1) – (2.5) дают связь между масштабными коэффициентами. Например, для масштабного коэффициента скорости α_ν

.

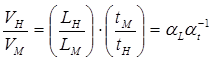Динамически подобными называются такие потоки, в которых выполняются следующие три условия:

1. В сходственных точках этих потоков действуют силы одной и той же природы.

2. Отношения между одноименными силами во всех сходственных точках потоков равны одной и той же величине.

3. Начальные и граничные условия в этих потоках тождественны и отличаются только масштабом задаваемых параметров.

Так как размерностью силы является произведение размерностей массы M = ρ · L³ и ускорения j = L · T ^–2 , т. е.

F = ρ · L³ ·L· T^-2 = ρL² · L2/T² =ρ · L² · V²,

то для динамического подобия необходимо соблюдение отношения

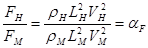Задача 2.1: Выразить масштабы подобия угловой скорости α_ω, объемного расхода α_Q, энергии α_E и мощности в зависимости от масштаба времени α_t, линейного масштаба α_L и масштаба плотности α_ρ.

Решение: Угловая скорость есть отношение радиана ко времени, поэтому ω ~ 1/t. Масштаб подобия угловой скорости будет равен ω_Н/ω_М = t_M/t_H = α_t^-1. Аналогично для расхода Q = V · S ~ L/t · L² ~ L³/t 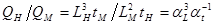. Для энергии получаем .

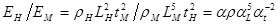Задача 2.2: Определить масштаб времени α_t, если модель судна, изготовленная в 1/100 натуральной величины, движется в 10 раз медленнее судна.

Решение: По условию задачи V_H/V_M = 10, V_H/V_M = α_L · α_t^-1. Окончательно α_L · α_t^-1 = 10 и α_t = ¹⁰⁰/₁₀ = 10.